Blog Archives
Chaos and the tide of Entropy!
We have discussed chaos. It is rooted in the fundamental idea that small changes in the initial condition in a system can amplify the impact on the final outcome in the system. Let us now look at another sibling in systems literature – namely, the concept of entropy. We will then attempt to bridge these two concepts since they are inherent in all systems.
Entropy arises from the law of thermodynamics. Let us state all three laws:
- First law is known as the Lay of Conservation of Energy which states that energy can neither be created nor destroyed: energy can only be transferred from one form to another. Thus, if there is work in terms of energy transformation in a system, there is equivalent loss of energy transformation around the system. This fact balances the first law of thermodynamics.
- Second law of thermodynamics states that the entropy of any isolated system always increases. Entropy always increases, and rarely ever decreases. If a locker room is not tidied, entropy dictates that it will become messier and more disorderly over time. In other words, all systems that are stagnant will inviolably run against entropy which would lead to its undoing over time. Over time the state of disorganization increases. While energy cannot be created or destroyed, as per the First Law, it certainly can change from useful energy to less useful energy.
- Third law establishes that the entropy of a system approaches a constant value as the temperature approaches absolute zero. Thus, the entropy of a pure crystalline substance at absolute zero temperature is zero. However, if there is any imperfection that resides in the crystalline structure, there will be some entropy that will act upon it.
Entropy refers to a measure of disorganization. Thus people in a crowd that is widely spread out across a large stadium has high entropy whereas it would constitute low entropy if people are all huddled in one corner of the stadium. Entropy is the quantitative measure of the process – namely, how much energy has been spent from being localized to being diffused in a system. Entropy is enabled by motion or interaction of elements in a system, but is actualized by the process of interaction. All particles work toward spontaneously dissipating their energy if they are not curtailed from doing so. In other words, there is an inherent will, philosophically speaking, of a system to dissipate energy and that process of dissipation is entropy. However, it makes no effort to figure out how quickly entropy kicks into gear – it is this fact that makes it difficult to predict the overall state of the system.
Chaos, as we have already discussed, makes systems unpredictable because of perturbations in the initial state. Entropy is the dissipation of energy in the system, but there is no standard way of knowing the parameter of how quickly entropy would set in. There are thus two very interesting elements in systems that almost work simultaneously to ensure that predictability of systems become harder.
Another way of looking at entropy is to view this as a tax that the system charges us when it goes to work on our behalf. If we are purposefully calibrating a system to meet a certain purpose, there is inevitably a corresponding usage of energy or dissipation of energy otherwise known as entropy that is working in parallel. A common example that we are familiar with is mass industrialization initiatives. Mass industrialization has impacts on environment, disease, resource depletion, and a general decay of life in some form. If entropy as we understand it is an irreversible phenomenon, then there is virtually nothing that can be done to eliminate it. It is a permanent tax of varying magnitude in the system.
Humans have since early times have tried to formulate a working framework of the world around them. To do that, they have crafted various models and drawn upon different analogies to lend credence to one way of thinking over another. Either way, they have been left best to wrestle with approximations: approximations associated with their understanding of the initial conditions, approximations on model mechanics, approximations on the tax that the system inevitably charges, and the approximate distribution of potential outcomes. Despite valiant efforts to reduce the framework to physical versus behavioral phenomena, their final task of creating or developing a predictable system has not worked. While physical laws of nature describe physical phenomena, the behavioral laws describe non-deterministic phenomena. If linear equations are used as tools to understand the physical laws following the principles of classical Newtonian mechanics, the non-linear observations marred any consistent and comprehensive framework for clear understanding. Entropy reaches out toward an irreversible thermal death: there is an inherent fatalism associated with the Second Law of Thermodynamics. However, if that is presumed to be the case, how is it that human evolution has jumped across multiple chasms and have evolved to what it is today? If indeed entropy is the tax, one could argue that chaos with its bounded but amplified mechanics have allowed the human race to continue.
Let us now deliberate on this observation of Richard Feynmann, a Nobel Laurate in physics – “So we now have to talk about what we mean by disorder and what we mean by order. … Suppose we divide the space into little volume elements. If we have black and white molecules, how many ways could we distribute them among the volume elements so that white is on one side and black is on the other? On the other hand, how many ways could we distribute them with no restriction on which goes where? Clearly, there are many more ways to arrange them in the latter case.
We measure “disorder” by the number of ways that the insides can be arranged, so that from the outside it looks the same. The logarithm of that number of ways is the entropy. The number of ways in the separated case is less, so the entropy is less, or the “disorder” is less.” It is commonly also alluded to as the distinction between microstates and macrostates. Essentially, it says that there could be innumerable microstates although from an outsider looking in – there is only one microstate. The number of microstates hints at the system having more entropy.
In a different way, we ran across this wonderful example: A professor distributes chocolates to students in the class. He has 35 students but he distributes 25 chocolates. He throws those chocolates to the students and some students might have more than others. The students do not know that the professor had only 25 chocolates: they have presumed that there were 35 chocolates. So the end result is that the students are disconcerted because they perceive that the other students have more chocolates than they have distributed but the system as a whole shows that there are only 25 chocolates. Regardless of all of the ways that the 25 chocolates are configured among the students, the microstate is stable.
So what is Feynmann and the chocolate example suggesting for our purpose of understanding the impact of entropy on systems: Our understanding is that the reconfiguration or the potential permutations of elements in the system that reflect the various microstates hint at higher entropy but in reality has no impact on the microstate per se except that the microstate has inherently higher entropy. Does this mean that the macrostate thus has a shorter life-span? Does this mean that the microstate is inherently more unstable? Could this mean an exponential decay factor in that state? The answer to all of the above questions is not always. Entropy is a physical phenomenon but to abstract this out to enable a study of organic systems that represent super complex macrostates and arrive at some predictable pattern of decay is a bridge too far! If we were to strictly follow the precepts of the Second Law and just for a moment forget about Chaos, one could surmise that evolution is not a measure of progress, it is simply a reconfiguration.
Theodosius Dobzhansky, a well known physicist, says: “Seen in retrospect, evolution as a whole doubtless had a general direction, from simple to complex, from dependence on to relative independence of the environment, to greater and greater autonomy of individuals, greater and greater development of sense organs and nervous systems conveying and processing information about the state of the organism’s surroundings, and finally greater and greater consciousness. You can call this direction progress or by some other name.”
Harold Mosowitz says “Life is organization. From prokaryotic cells, eukaryotic cells, tissues and organs, to plants and animals, families, communities, ecosystems, and living planets, life is organization, at every scale. The evolution of life is the increase of biological organization, if it is anything. Clearly, if life originates and makes evolutionary progress without organizing input somehow supplied, then something has organized itself. Logical entropy in a closed system has decreased. This is the violation that people are getting at, when they say that life violates the second law of thermodynamics. This violation, the decrease of logical entropy in a closed system, must happen continually in the Darwinian account of evolutionary progress.”
Entropy occurs in all systems. That is an indisputable fact. However, if we start defining boundaries, then we are prone to see that these bounded systems decay faster. However, if we open up the system to leave it unbounded, then there are a lot of other forces that come into play that is tantamount to some net progress. While it might be true that energy balances out, what we miss as social scientists or model builders or avid students of systems – we miss out on indices that reflect on leaps in quality and resilience and a horde of other factors that stabilizes the system despite the constant and ominous presence of entropy’s inner workings.
History of Chaos
| Chaos is inherent in all compounded things. Strive on with diligence! –Buddha |
Scientific theories are characterized by the fact that they are open to refutation. To create a scientific model, there are three successive steps that one follows: observe the phenomenon, translate that into equations, and then solve the equations.
One of the early philosophers of science, Karl Popper (1902-1994) discussed this at great length in his book – The Logic of Scientific Discovery. He distinguishes scientific theories from metaphysical or mythological assertions. His main theses is that a scientific theory must be open to falsification: it has to be reproducible separately and yet one can gather data points that might refute the fundamental elements of theory. Developing a scientific theory in a manner that can be falsified by observations would result in new and more stable theories over time. Theories can be rejected in favor of a rival theory or a calibration of the theory in keeping with the new set of observations and outcomes that the theories posit. Until Popper’s time and even after, social sciences have tried to work on a framework that would allow the construction of models that would formulate some predictive laws that govern social dynamics. In his book, Poverty of Historicism, Popper maintained that such an endeavor is not fruitful since it does not take into consideration the myriad of minor elements that interact closely with one another in a meaningful way. Hence, he has touched indirectly on the concept of chaos and complexity and how it touches the scientific method. We will now journey into the past and through the present to understand the genesis of the theory and how it has been channelized by leading scientists and philosophers to decipher a framework for study society and nature.
As we have already discussed, one of the main pillars of Science is determinism: the probability of prediction. It holds that every event is determined by natural laws. Nothing can happen without an unbroken chain of causes that can be traced all the way back to an initial condition. The deterministic nature of science goes all the way back to Aristotelian times. Interestingly, Aristotle argued that there is some degree of indeterminism and he relegated this to chance or accidents. Chance is a character that makes its presence felt in every plot in the human and natural condition. Aristotle wrote that “we do not have knowledge of a thing until we have grasped its why, that is to say, its cause.” He goes on to illustrate his idea in greater detail – namely, that the final outcome that we see in a system is on account of four kinds of influencers: Matter, Form, Agent and Purpose.
Matter is what constitutes the outcome. For a chair it might be wood. For a statue, it might be marble. The outcome is determined by what constitutes the outcome.
Form refers to the shape of the outcome. Thus, a carpenter or a sculptor would have a pre-conceived notion of the shape of the outcome and they would design toward that artifact.
Agent refers to the efficient cause or the act of producing the outcome. Carpentry or masonry skills would be important to shape the final outcome.
Finally, the outcome itself must serve a purpose on its own. For a chair, it might be something to sit on, for a statue it might be something to be marveled at.
However, Aristotle also admits that luck and chance can play an important role that do not fit the causal framework in its own right. Some things do happen by chance or luck. Chance is a rare event, it is a random event and it is typically brought out by some purposeful action or by nature.
We had briefly discussed the Laplace demon and he summarized this wonderfully: “We ought then to consider the resent state of the universe as the effect of its previous state and as the cause of that which is to follow. An intelligence that, at a given instant, could comprehend all the forces by which nature is animated and the respective situation of the beings that make it up if moreover it were vast enough to submit these data to analysis, would encompass in the same formula the movements of the greatest bodies of the universe and those of the lightest atoms. For such an intelligence nothing would be uncertain, and the future, like the past, would be open to its eyes.” He thus admits to the fact that we lack the vast intelligence and we are forced to use probabilities in order to get a sense of understanding of dynamical systems.
It was Maxwell in his pivotal book “Matter and Motion” published in 1876 lay the groundwork of chaos theory.
“There is a maxim which is often quoted, that “the same causes will always produce the same effects.’ To make this maxim intelligible we must define what we mean by the same causes and the same effects, since it is manifest that no event ever happens more than once, so that the causes and effects cannot be the same in all respects. There is another maxim which must not be confounded with that quoted at the beginning of this article, which asserts “That like causes produce like effects.” This is only true when small variations in the initial circumstances produce only small variations in the final state of the system. In a great many physical phenomena this condition is satisfied: but there are other cases in which a small initial variation may produce a great change in the final state of the system, as when the displacement of the points cause a railway train to run into another instead of keeping its proper course.” What is interesting however in the above quote is that Maxwell seems to go with the notion that in a great many cases there is no sensitivity to initial conditions.
In the 1890’s Henri Poincare was the first exponent of chaos theory. He says “it may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible.” This was a far cry from the Newtonian world which sought order on how the solar system worked. Newton’s model was posted on the basis of the interaction between just two bodies. What would then happen if three bodies or N bodies were introduced into the model. This led to the rise of the Three Body Problem which led to Poincare embracing the notion that this problem could not be solved and can be tackled by approximate numerical techniques. Solving this resulted in solutions that were so tangled that is was difficult to not only draw them, it was near impossible to derive equations to fit the results. In addition, Poincare also discovered that if the three bodies started from slightly different initial positions, the orbits would trace out different paths. This led to Poincare forever being designated as the Father of Chaos Theory since he laid the groundwork on the most important element in chaos theory which is the sensitivity to initial dependence.
In the early 1960’s, the first true experimenter in chaos was a meteorologist named Edward Lorenz. He was working on a problem in weather prediction and he set up a system with twelve equations to model the weather. He set the initial conditions and the computer was left to predict what the weather might be. Upon revisiting this sequence later on, he inadvertently and by sheer accident, decided to run the sequence again in the middle and he noticed that the outcome was significantly different. The imminent question that followed was why the outcome was so different than the original. He traced this back to the initial condition wherein he noted that the initial input was different with respect to the decimal places. The system incorporated the all of the decimal places rather than the first three. (He had originally input the number .506 and he had concatenated the number from .506127). He would have expected that this thin variation in input would have created a sequence close to the original sequence but that was not to be: it was distinctly and hugely different. This effect became known as the Butterfly effect which is often substituted for Chaos Theory. Ian Stewart in his book, Does God Play Dice? The Mathematics of Chaos, describes this visually as follows:
“The flapping of a single butterfly’s wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month’s time, a tornado that would have devastated the Indonesian cost doesn’t happen. Or maybe one that wasn’t going to happen, does.”
Lorenz thus argued that it would be impossible to predict the weather accurately. However, he reduced his experiment to fewer set of equations and took upon observations of how small change in initial conditions affect predictability of smaller systems. He found a parallel – namely, that changes in initial conditions tends to render the final outcome of a system to be inaccurate. As he looked at alternative systems, he found a strange pattern that emerged – namely, that the system always represented a double spiral – the system never settled down to a single point but they never repeated its trajectory. It was a path breaking discovery that led to further advancement in the science of chaos in later years.
Years later, Robert May investigated how this impacts population. He established an equation that reflected a population growth and initialized the equation with a parameter for growth rate value. (The growth rate was initialized to 2.7). May found that as he increased the parameter value, the population grew which was expected. However, once he passed the 3.0 growth value, he noticed that equation would not settle down to a single population but branch out to two different values over time. If he raised the initial value more, the bifurcation or branching of the population would be twice as much or four different values. If he continued to increase the parameter, the lines continue to double until chaos appeared and it became hard to make point predictions.
There was another innate discovery that occurred through the experiment. When one visually looks at the bifurcation, one tends to see similarity between the small and large branches. This self-similarity became an important part of the development of chaos theory.
Benoit Mandelbrot started to study this self-similarity pattern in chaos. He was an economist and he applied mathematical equations to predict fluctuations in cotton prices. He noted that particular price changes were not predictable but there were certain patterns that were repeated and the degree of variation in prices had remained largely constant. This is suggestive of the fact that one might, upon preliminary reading of chaos, arrive at the notion that if weather cannot be predictable, then how can we predict climate many years out. On the contrary, Mandelbrot’s experiments seem to suggest that short time horizons are difficult to predict that long time horizon impact since systems tend to settle into some patterns that is reflecting of smaller patterns across periods. This led to the development of the concept of fractal dimensions, namely that sub-systems develop a symmetry to a larger system.
Feigenbaum was a scientist who became interested in how quickly bifurcations occur. He discovered that regardless of the scale of the system, the came at a constant rate of 4.669. If you reduce or enlarge the scale by that constant, you would see the mechanics at work which would lead to an equivalence in self-similarity. He applied this to a number of models and the same scaling constant took effect. Feigenbaum had established, for the first time, a universal constant around chaos theory. This was important because finding a constant in the realm of chaos theory was suggestive of the fact that chaos was an ordered process, not a random one.
Sir James Lighthill gave a lecture and in that he made an astute observation –
“We are all deeply conscious today that the enthusiasm of our forebears for the marvelous achievements of Newtonian mechanics led them to make generalizations in this area of predictability which, indeed, we may have generally tended to believe before 1960, but which we now recognize were false. We collectively wish to apologize for having misled the general educated public by spreading ideas about determinism of systems satisfying Newton’s laws of motion that, after 1960, were to be proved incorrect.”
Distribution Economics
Distribution is a method to get products and services to the maximum number of customers efficiently.
Complexity science is the study of complex systems and the problems that are multi-dimensional, dynamic and unpredictable. It constitutes a set of interconnected relationships that are not always abiding to the laws of cause and effect, but rather the modality of non-linearity. Thomas Kuhn in his pivotal essay: The Structure of Scientific Revolutions posits that anomalies that arise in scientific method rise to the level where it can no longer be put on hold or simmer on a back-burner: rather, those anomalies become the front line for new methods and inquiries such that a new paradigm necessarily must emerge to supplant the old conversations. It is this that lays the foundation of scientific revolution – an emergence that occurs in an ocean of seeming paradoxes and competing theories. Contrary to a simple scientific method that seeks to surface regularities in natural phenomenon, complexity science studies the effects that rules have on agents. Rules do not drive systems toward a predictable outcome: rather it sets into motion a high density of interactions among agents such that the system coalesces around a purpose: that being necessarily that of survival in context of its immediate environment. In addition, the learnings that follow to arrive at the outcome is then replicated over periods to ensure that the systems mutate to changes in the external environment. In theory, the generative rules leads to emergent behavior that displays patterns of parallelism to earlier known structures.
For any system to survive and flourish, distribution of information, noise and signals in and outside of a CPS or CAS is critical. We have touched at length that the system comprises actors and agents that work cohesively together to fulfill a special purpose. Specialization and scale matter! How is a system enabled to fulfill their purpose and arrive at a scale that ensures long-term sustenance? Hence the discussion on distribution and scale which is a salient factor in emergence of complex systems that provide the inherent moat of “defensibility” against internal and external agents working against it.
Distribution, in this context, refers to the quality and speed of information processing in the system. It is either created by a set of rules that govern the tie-ups between the constituent elements in the system or it emerges based on a spontaneous evolution of communication protocols that are established in response to internal and external stimuli. It takes into account the available resources in the system or it sets up the demands on resource requirements. Distribution capabilities have to be effective and depending upon the dynamics of external systems, these capabilities might have to be modified effectively. Some distribution systems have to be optimized or organized around efficiency: namely, the ability of the system to distribute information efficiently. On the other hand, some environments might call for less efficiency as the key parameter, but rather focus on establishing a scale – an escape velocity in size and interaction such that the system can dominate the influence of external environments. The choice between efficiency and size is framed by the long-term purpose of the system while also accounting for the exigencies of ebbs and flows of external agents that might threaten the system’s existence.
Since all systems are subject to the laws of entropy and the impact of unintended consequences, strategies have to be orchestrated accordingly. While it is always naïve to assume exactitude in the ultimate impact of rules and behavior, one would surmise that such systems have to be built around the fault lines of multiple roles for agents or group of agents to ensure that the system is being nudged, more than less, toward the desired outcome. Hence, distribution strategy is the aggregate impact of several types of channels of information that are actively working toward a common goal. The idea is to establish multiple channels that invoke different strategies while not cannibalizing or sabotaging an existing set of channels. These mutual exclusive channels have inherent properties that are distinguished by the capacity and length of the channels, the corresponding resources that the channels use and the sheer ability to chaperone the system toward the overall purpose.
The complexity of the purpose and the external environment determines the strategies deployed and whether scale or efficiency are the key barometers for success. If a complex system must survive and hopefully replicate from strength to greater strength over time, size becomes more paramount than efficiency. Size makes up for the increased entropy which is the default tax on the system, and it also increases the possibility of the system to reach the escape velocity. To that end, managing for scale by compromising efficiency is a perfectly acceptable means since one is looking at the system with a long-term lens with built-in regeneration capabilities. However, not all systems might fall in this category because some environments are so dynamic that planning toward a long-term stability is not practical, and thus one has to quickly optimize for increased efficiency. It is thus obvious that scale versus efficiency involves risky bets around how the external environment will evolve. We have looked at how the systems interact with external environments: yet, it is just as important to understand how the actors work internally in a system that is pressed toward scale than efficiency, or vice versa. If the objective is to work toward efficiency, then capabilities can be ephemeral: one builds out agents and actors with capabilities that are mission-specific. On the contrary, scale driven systems demand capabilities that involve increased multi-tasking abilities, the ability to develop and learn from feedback loops, and to prime the constraints with additional resources. Scaling demand acceleration and speed: if a complex system can be devised to distribute information and learning at an accelerating pace, there is a greater likelihood that this system would dominate the environment.
Scaling systems can be approached by adding more agents with varying capabilities. However, increased number of participants exponentially increase the permutations and combinations of channels and that can make the system sluggish. Thus, in establishing the purpose and the subsequent design of the system, it is far more important to establish the rules of engagement. Further, the rules might have some centralized authority that will directionally provide the goal while other rules might be framed in a manner to encourage a pure decentralization of authority such that participants act quickly in groups and clusters to enable execution toward a common purpose.
In business we are surrounded by uncertainty and opportunities. It is how we calibrate around this that ultimately reflects success. The ideal framework at work would be as follows:
- What are the opportunities and what are the corresponding uncertainties associated with the opportunities? An honest evaluation is in order since this is what sets the tone for the strategic framework and direction of the organization.
- Should we be opportunistic and establish rules that allow the system to gear toward quick wins: this would be more inclined toward efficiencies. Or should we pursue dominance by evaluating our internal capability and the probability of winning and displacing other systems that are repositioning in advance or in response to our efforts? At which point, speed and scale become the dominant metric and the resources and capabilities and the set of governing rules have to be aligned accordingly.
- How do we craft multiple channels within and outside of the system? In business lingo, that could translate into sales channels. These channels are selling products and services and can be adding additional value along the way to the existing set of outcomes that the system is engineered for. The more the channels that are mutually exclusive and clearly differentiated by their value propositions, the stronger the system and the greater the ability to scale quickly. These antennas, if you will, also serve to be receptors for new information which will feed data into the organization which can subsequently process and reposition, if the situation so warrants. Having as many differentiated antennas comprise what constitutes the distribution strategy of the organization.
- The final cut is to enable a multi-dimensional loop between external and internal system such that the system expands at an accelerating pace without much intervention or proportionate changes in rules. In other words, system expands autonomously – this is commonly known as the platform effect. Scale does not lead to platform effect although the platform effect most definitely could result in scale. However, scale can be an important contributor to platform effect, and if the latter gets root, then the overall system achieves efficiency and scale in the long run.
Network Theory and Network Effects
Complexity theory needs to be coupled with network theory to get a more comprehensive grasp of the underlying paradigms that govern the outcomes and morphology of emergent systems. In order for us to understand the concept of network effects which is commonly used to understand platform economics or ecosystem value due to positive network externalities, we would like to take a few steps back and appreciate the fundamental theory of networks. This understanding will not only help us to understand complexity and its emergent properties at a low level but also inform us of the impact of this knowledge on how network effects can be shaped to impact outcomes in an intentional manner.
There are first-order conditions that must be met to gauge whether the subject of the observation is a network. Firstly, networks are all about connectivity within and between systems. Understanding the components that bind the system would be helpful. However, do keep in mind that complexity systems (CPS and CAS) might have emergent properties due to the association and connectivity of the network that might not be fully explained by network theory. All the same, understanding networking theory is a building block to understanding emergent systems and the outcome of its structure on addressing niche and macro challenges in society.
Networks operates spatially in a different space and that has been intentionally done to allow some simplification and subsequent generalization of principles. The geometry of network is called network topology. It is a 2D perspective of connectivity.
Networks are subject to constraints (physical resources, governance constraint, temporal constraints, channel capacity, absorption and diffusion of information, distribution constraint) that might be internal (originated by the system) or external (originated in the environment that the network operates in).
Finally, there is an inherent non-linearity impact in networks. As nodes increase linearly, connections will increase exponentially but might be subject to constraints. The constraints might define how the network structure might morph and how information and signals might be processed differently.
Graph theory is the most widely used tool to study networks. It consists of four parts: vertices which represent an element in the network, edges refer to relationship between nodes which we call links, directionality which refers to how the information is passed ( is it random and bi-directional or follows specific rules and unidirectional), channels that refer to bandwidth that carry information, and finally the boundary which establishes specificity around network operations. A graph can be weighted – namely, a number can be assigned to each length to reflect the degree of interaction or the strength of resources or the proximity of the nodes or the ordering of discernible clusters.
The central concept of network theory thus revolves around connectivity between nodes and how non-linear emergence occurs. A node can have multiple connections with other node/nodes and we can weight the node accordingly. In addition, the purpose of networks is to pass information in the most efficient manner possible which relays into the concept of a geodesic which is either the shortest path between two nodes that must work together to achieve a purpose or the least number of leaps through links that information must negotiate between the nodes in the network.
Technically, you look for the longest path in the network and that constitutes the diameter while you calculate the average path length by examining the shortest path between nodes, adding all of those paths up and then dividing by the number of pairs. Significance of understanding the geodesic allows an understanding of the size of the network and throughput power that the network is capable of.
Nodes are the atomic elements in the network. It is presumed that its degree of significance is related to greater number of connections. There are other factors that are important considerations: how adjacent or close are the nodes to one another, does some nodes have authority or remarkable influence on others, are nodes positioned to be a connector between other nodes, and how capable are the nodes in absorbing, processing and diffusing the information across the links or channels. How difficult is it for the agents or nodes in the network to make connections? It is presumed that if the density of the network is increased, then we create a propensity in the overall network system to increase the potential for increased connectivity.
As discussed previously, our understanding of the network is deeper once we understand the elements well. The structure or network topology is represented by the graph and then we must understand size of network and the patterns that are manifested in the visual depiction of the network. Patterns, for our purposes, might refer to clusters of nodes that are tribal or share geographical proximity that self-organize and thus influence the structure of the network. We will introduce a new term homophily where agents connect with those like themselves. This attribute presumably allows less resources needed to process information and diffuse outcomes within the cluster. Most networks have a cluster bias: in other words, there are areas where there is increased activity or increased homogeneity in attributes or some form of metric that enshrines a group of agents under one specific set of values or activities. Understanding the distribution of cluster and the cluster bias makes it easier to influence how to propagate or even dismantle the network. This leads to an interesting question: Can a network that emerges spontaneously from the informal connectedness between agents be subjected to some high dominance coefficient – namely, could there be nodes or links that might exercise significant weight on the network?
The network has to align to its environment. The environment can place constraints on the network. In some instances, the agents have to figure out how to overcome or optimize their purpose in the context of the presence of the environmental constraints. There is literature that suggests the existence of random networks which might be an initial state, but it is widely agreed that these random networks self-organize around their purpose and their interaction with its environment. Network theory assigns a number to the degree of distribution which means that all or most nodes have an equivalent degree of connectivity and there is no skewed influence being weighed on the network by a node or a cluster. Low numbers assigned to the degree of distribution suggest a network that is very democratic versus high number that suggests centralization. To get a more practical sense, a mid-range number assigned to a network constitutes a decentralized network which has close affinities and not fully random. We have heard of the six degrees of separation and that linkage or affinity is most closely tied to a mid-number assignment to the network.
We are now getting into discussions on scale and binding this with network theory. Metcalfe’s law states that the value of a network grows as a square of the number of the nodes in the network. More people join the network, the more valuable the network. Essentially, there is a feedback loop that is created, and this feedback loop can kindle a network to grow exponentially. There are two other topics – Contagion and Resilience. Contagion refers to the ability of the agents to diffuse information. This information can grow the network or dismantle it. Resilience refers to how the network is organized to preserve its structure. As you can imagine, they have huge implications that we see. How do certain ideas proliferate over others, how does it cluster and create sub-networks which might grow to become large independent networks and how it creates natural defense mechanisms against self-immolation and destruction?
Network effect is commonly known as externalities in economics. It is an effect that is external to the transaction but influences the transaction. It is the incremental benefit gained by an existing user for each new user that joins the network. There are two types of network effects: Direct network effects and Indirect network effect. Direct network effects are same side effects. The value of a service goes up as the number of users goes up. For example, if more people have phones, it is useful for you to have a phone. The entire value proposition is one-sided. Indirect networks effects are multi-sided. It lends itself to our current thinking around platforms and why smart platforms can exponentially increase the network. The value of the service increases for one user group when a new user group joins the network. Take for example the relationship between credit card banks, merchants and consumers. There are three user groups, and each gather different value from the network of agents that have different roles. If more consumers use credit cards to buy, more merchants will sign up for the credit cards, and as more merchants sign up – more consumers will sign up with the bank to get more credit cards. This would be an example of a multi-sided platform that inherently has multi-sided network effects. The platform inherently gains significant power such that it becomes more valuable for participants in the system to join the network despite the incremental costs associated with joining the network. Platforms that are built upon effective multi-sided network effects grow quickly and are generally sustainable. Having said that, it could be just as easy that a few dominant bad actors in the network can dismantle and unravel the network completely. We often hear of the tipping point: namely, that once the platform reaches a critical mass of users, it would be difficult to dismantle it. That would certainly be true if the agents and services are, in the aggregate, distributed fairly across the network: but it is also possible that new networks creating even more multi-sided network effects could displace an entrenched network. Hence, it is critical that platform owners manage the quality of content and users and continue to look for more opportunities to introduce more user groups to entrench and yet exponentially grow the network.
Managing Scale
| I think the most difficult thing had been scaling the infrastructure. Trying to support the response we had received from our users and the number of people that were interested in using the software. – Shawn Fanning |
Froude’s number? It is defined as the square of the ship’s velocity divided by its length and multiplied by the acceleration caused by gravity. So why are we introducing ships in this chapter? As I have done before, I am liberally standing on the shoulder of the giant, Geoffrey West, and borrowing from his account on the importance of the Froude’s number and the practical implications. Since ships are subject to turbulence, using a small model that works in a simulated turbulent environment might not work when we manufacture a large ship that is facing the ebbs and troughs of a finicky ocean. The workings and impact of turbulence is very complex, and at scale it becomes even more complex. Froude’s key contribution was to figure out a mathematical pathway of how to efficiently and effectively scale from a small model to a practical object. He did that by using a ratio as the common denominator. Mr. West provides an example that hits home: How fast does a 10-foot-long ship have to move to mimic the motion of a 700-foot-long ship moving at 20 knots. If they are to have the same Froude number (that is, the same value of the square of their velocity divided by their length), then the velocity has to scale as the square root of their lengths. The ratio of the square root of their lengths is the the square of 700 feet of the ship/10 feet of the model ship which turns out to be the square of 70. For the 10-foot model to mimic the motion of a large ship, it must move at the speed of 20 knots/ square of 70 or 2.5 knots. The Froude number is still widely used across many fields today to bridge small scale and large-scale thinking. Although this number applies to physical systems, the notion that adaptive systems can be similarly bridged through appropriate mathematical equations. Unfortunately, because of the increased number of variables impacting adaptive systems and all of these variables working and learning from one another, the task of establishing a Froude number becomes diminishingly small.
The other concept that has gained wide attention is the science of allometry. Allometry essentially states that as size increases, then the form of the object would change. Allometric scaling governs all complex physical and adaptive systems. So the question is whether there are some universal laws or mathematics that can be used to enable us to better understand or predict scale impacts. Let us extend this thinking a bit further. If sizes influence form and form constitute all sub-physical elements, then it would stand to reason that a universal law or a set of equations can provide deep explanatory powers on scale and systems. One needs to bear in mind that even what one might consider a universal law might be true within finite observations and boundaries. In other words, if there are observations that fall outside of those boundaries, one is forced into resetting our belief in the universal law or to frame a new paradigm to cover these exigencies. I mention this because as we seek to understand business and global grand challenges considering the existence of complexity, scale, chaos and seeming disorder – we might also want to embrace multiple laws or formulations working at different hierarchies and different data sets to arrive at satisficing solutions to the problems that we want to wrestle with.
Physics and mathematics allow a qualitatively high degree of predictability. One can craft models across different scales to make a sensible approach on how to design for scale. If you were to design a prototype using a 3D printer and decide to scale that prototype a 100X, there are mathematical scalar components that are factored into the mechanics to allow for some sort of equivalence which would ultimately lead to the final product fulfilling its functional purpose in a complex physical system. But how does one manage scale in light of those complex adaptive systems that emerge due to human interactions, evolution of organization, uncertainty of the future, and dynamic rules that could rapidly impact the direction of a company?
Is scale a single measure? Or is it a continuum? In our activities, we intentionally or unintentionally invoke scale concepts. What is the most efficient scale to measure an outcome, so we can make good policy decisions, how do we apply our learning from one scale to a system that operates on another scale and how do we assess how sets of phenomena operate at different scales, spatially and temporally, and how they impact one another? Now the most interesting question: Is scale polymorphous? Does the word scale have different meanings in different contexts? When we talk about microbiology, we are operating at micro-scales. When we talk at a very macro level, our scales are huge. In business, we regard scale with respect to how efficiently we grow. In one way, it is a measure but for the following discussion, we will interpret scale as non-linear growth expending fewer and fewer resources to support that growth as a ratio.
As we had discussed previously, complex adaptive systems self-organize over time. They arrive at some steady state outcome without active intervention. In fact, the active intervention might lead to unintended consequences that might even spell doom for the system that is being influenced. So as an organization scales, it is important to keep this notion of rapid self-organization in mind which will inform us to make or not make certain decisions from a central or top-down perspective. In other words, part of managing scale successfully is to not manage it at a coarse-grained level.
The second element of successfully managing scale is to understand the constraints that prevent scale. There is an entire chapter dedicated to the theory of constraints which sheds light on why this is a fundamental process management technique that increases the pace of the system. But for our purposes in this section, we will summarize as follows: every system as it grows have constraints. It is important to understand the constraints because these constraints slow the system: the bottlenecks have to be removed. And once one constraint is removed, then one comes across another constraint. The system is a chain of events and it is imperative that all of these events are identified. The weakest links harangue the systems and these weakest links have to be either cleared or resourced to enable the system to scale. It is a continuous process of observation and tweaking the results with the established knowledge that the demons of uncertainty and variability can reset the entire process and one might have to start again. Despite that fact, constraint management is an effective method to negotiate and manage scale.
The third element is devising the appropriate organization architecture. As one projects into the future, management might be inclined toward developing and investing in the architecture early to accommodate the scale. Overinvestment in the architecture might not be efficient. As mentioned, cities and social systems that grow 100% require 85% investment in infrastructure: in other words, systems grow on a sublinear scale from an infrastructure perspective. How does management of scale arrive at the 85%? It is nigh impossible, but it is important to reserve that concept since it informs management to architect the infrastructure cautiously. Large investments upfront could be a waste or could slow the system down: alternative, investments that are postponed a little too late can also impact the system adversely.
The fourth element of managing scale is to focus your lens of opportunity. In macroecology, we can arrive at certain conclusions when we regard the system from a distance versus very closely. We can subsume our understanding into one big bucket called climate change and then we figure out different ways to manage the complexity that causes the climate change by invoking certain policies and incentives at a macro level. However, if we go closer, we might decide to target a very specific contributor to climate change – namely, fossil fuels. The theory follows that to manage the dynamic complexity and scale of climate impact – it would be best to address a major factor which, in this case, would be fossil fuels. The equivalence of this in a natural business setting would be to establish and focus the strategy for scale in a niche vertical or a relatively narrower set of opportunities. Even though we are working in the web of complex adaptive systems, we might devise strategies to directionally manage the business within the framework of complex physical systems where we have an understanding of the slight variations of initial state and the realization that the final outcome might be broad but yet bounded for intentional management.
The final element is the management of initial states. Complex physical systems are governed by variation in initial states. Perturbation of these initial states can lead to a wide divergence of outcomes, albeit bounded within a certain frame of reference. It is difficult perhaps to gauge all the interactions that might occur from a starting point to the outcome, although we agree that a few adjustments like decentralization of decision making, constraint management, optimal organization structure and narrowing the playing field would be helpful.
Internal versus External Scale
This article discusses internal and external complexity before we tee up a more detailed discussion on internal versus external scale. This chapter acknowledges that complex adaptive systems have inherent internal and external complexities which are not additive. The impact of these complexities is exponential. Hence, we have to sift through our understanding and perhaps even review the salient aspects of complexity science which have already been covered in relatively more detail in earlier chapter. However, revisiting complexity science is important, and we will often revisit this across other blog posts to really hit home the fundamental concepts and its practical implications as it relates to management and solving challenges at a business or even a grander social scale.
A complex system is a part of a larger environment. It is a safe to say that the larger environment is more complex than the system itself. But for the complex system to work, it needs to depend upon a certain level of predictability and regularity between the impact of initial state and the events associated with it or the interaction of the variables in the system itself. Note that I am covering both – complex physical systems and complex adaptive systems in this discussion. A system within an environment has an important attribute: it serves as a receptor to signals of external variables of the environment that impact the system. The system will either process that signal or discard the signal which is largely based on what the system is trying to achieve. We will dedicate an entire article on system engineering and thinking later, but the uber point is that a system exists to serve a definite purpose. All systems are dependent on resources and exhibits a certain capacity to process information. Hence, a system will try to extract as many regularities as possible to enable a predictable dynamic in an efficient manner to fulfill its higher-level purpose.
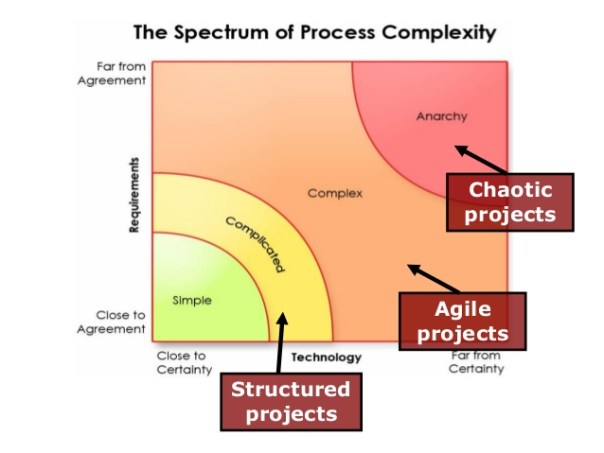
Let us understand external complexities. We can interchangeably use the word environmental complexity as well. External complexity represents physical, cultural, social, and technological elements that are intertwined. These environments beleaguered with its own grades of complexity acts as a mold to affect operating systems that are mere artifacts. If operating systems can fit well within the mold, then there is a measure of fitness or harmony that arises between an internal complexity and external complexity. This is the root of dynamic adaptation. When external environments are very complex, that means that there are a lot of variables at play and thus, an internal system has to process more information in order to survive. So how the internal system will react to external systems is important and they key bridge between those two systems is in learning. Does the system learn and improve outcomes on account of continuous learning and does it continually modify its existing form and functional objectives as it learns from external complexity? How is the feedback loop monitored and managed when one deals with internal and external complexities? The environment generates random problems and challenges and the internal system has to accept or discard these problems and then establish a process to distribute the problems among its agents to efficiently solve those problems that it hopes to solve for. There is always a mechanism at work which tries to align the internal complexity with external complexity since it is widely believed that the ability to efficiently align the systems is the key to maintaining a relatively competitive edge or intentionally making progress in solving a set of important challenges.
Internal complexity are sub-elements that interact and are constituents of a system that resides within the larger context of an external complex system or the environment. Internal complexity arises based on the number of variables in the system, the hierarchical complexity of the variables, the internal capabilities of information pass-through between the levels and the variables, and finally how it learns from the external environment. There are five dimensions of complexity: interdependence, diversity of system elements, unpredictability and ambiguity, the rate of dynamic mobility and adaptability, and the capability of the agents to process information and their individual channel capacities.
If we are discussing scale management, we need to ask a fundamental question. What is scale in the context of complex systems? Why do we manage for scale? How does management for scale advance us toward a meaningful outcome? How does scale compute in internal and external complex systems? What do we expect to see if we have managed for scale well? What does the future bode for us if we assume that we have optimized for scale and that is the key objective function that we have to pursue?
Model Thinking
| Model Framework |
The fundamental tenet of theory is the concept of “empiria“. Empiria refers to our observations. Based on observations, scientists and researchers posit a theory – it is part of scientific realism.
A scientific model is a causal explanation of how variables interact to produce a phenomenon, usually linearly organized. A model is a simplified map consisting of a few, primary variables that is gauged to have the most explanatory powers for the phenomenon being observed. We discussed Complex Physical Systems and Complex Adaptive Systems early on this chapter. It is relatively easier to map CPS to models than CAS, largely because models become very unwieldy as it starts to internalize more variables and if those variables have volumes of interaction between them. A simple analogy would be the use of multiple regression models: when you have a number of independent variables that interact strongly between each other, autocorrelation errors occur, and the model is not stable or does not have predictive value.
Research projects generally tend to either look at a case study or alternatively, they might describe a number of similar cases that are logically grouped together. Constructing a simple model that can be general and applied to many instances is difficult, if not impossible. Variables are subject to a researcher’s lack of understanding of the variable or the volatility of the variable. What further accentuates the problem is that the researcher misses on the interaction of how the variables play against one another and the resultant impact on the system. Thus, our understanding of our system can be done through some sort of model mechanics but, yet we share the common belief that the task of building out a model to provide all of the explanatory answers are difficult, if not impossible. Despite our understanding of our limitations of modeling, we still develop frameworks and artifact models because we sense in it a tool or set of indispensable tools to transmit the results of research to practical use cases. We boldly generalize our findings from empiria into general models that we hope will explain empiria best. And let us be mindful that it is possible – more so in the CAS systems than CPS that we might have multiple models that would fight over their explanatory powers simply because of the vagaries of uncertainty and stochastic variations.
Popper says: “Science does not rest upon rock-bottom. The bold structure of its theories rises, as it were, above a swamp. It is like a building erected on piles. The piles are driven down from above into the swamp, but not down to any natural or ‘given’ base; and when we cease our attempts to drive our piles into a deeper layer, it is not because we have reached firm ground. We simply stop when we are satisfied that they are firm enough to carry the structure, at least for the time being”. This leads to the satisficing solution: if a model can choose the least number of variables to explain the greatest amount of variations, the model is relatively better than other models that would select more variables to explain the same. In addition, there is always a cost-benefit analysis to be taken into consideration: if we add x number of variables to explain variation in the outcome but it is not meaningfully different than variables less than x, then one would want to fall back on the less-variable model because it is less costly to maintain.
Researchers must address three key elements in the model: time, variation and uncertainty. How do we craft a model which reflects the impact of time on the variables and the outcome? How to present variations in the model? Different variables might vary differently independent of one another. How do we present the deviation of the data in a parlance that allows us to make meaningful conclusions regarding the impact of the variations on the outcome? Finally, does the data that is being considered are actual or proxy data? Are the observations approximate? How do we thus draw the model to incorporate the fuzziness: would confidence intervals on the findings be good enough?
Two other equally other concepts in model design is important: Descriptive Modeling and Normative Modeling.
Descriptive models aim to explain the phenomenon. It is bounded by that goal and that goal only.
There are certain types of explanations that they fall back on: explain by looking at data from the past and attempting to draw a cause and effect relationship. If the researcher is able to draw a complete cause and effect relationship that meets the test of time and independent tests to replicate the results, then the causality turns into law for the limited use-case or the phenomenon being explained. Another explanation method is to draw upon context: explaining a phenomenon by looking at the function that the activity fulfills in its context. For example, a dog barks at a stranger to secure its territory and protect the home. The third and more interesting type of explanation is generally called intentional explanation: the variables work together to serve a specific purpose and the researcher determines that purpose and thus, reverse engineers the understanding of the phenomenon by understanding the purpose and how the variables conform to achieve that purpose.
This last element also leads us to thinking through the other method of modeling – namely, normative modeling. Normative modeling differs from descriptive modeling because the target is not to simply just gather facts to explain a phenomenon, but rather to figure out how to improve or change the phenomenon toward a desirable state. The challenge, as you might have already perceived, is that the subjective shadow looms high and long and the ultimate finding in what would be a normative model could essentially be a teleological representation or self-fulfilling prophecy of the researcher in action. While this is relatively more welcome in a descriptive world since subjectivism is diffused among a larger group that yields one solution, it is not the best in a normative world since variation of opinions that reflect biases can pose a problem.
How do we create a representative model of a phenomenon? First, we weigh if the phenomenon is to be understood as a mere explanation or to extend it to incorporate our normative spin on the phenomenon itself. It is often the case that we might have to craft different models and then weigh one against the other that best represents how the model can be explained. Some of the methods are fairly simple as in bringing diverse opinions to a table and then agreeing upon one specific model. The advantage of such an approach is that it provides a degree of objectivism in the model – at least in so far as it removes the divergent subjectivity that weaves into the various models. Other alternative is to do value analysis which is a mathematical method where the selection of the model is carried out in stages. You define the criteria of the selection and then the importance of the goal (if that be a normative model). Once all of the participants have a general agreement, then you have the makings of a model. The final method is to incorporate all all of the outliers and the data points in the phenomenon that the model seeks to explain and then offer a shared belief into those salient features in the model that would be best to apply to gain information of the phenomenon in a predictable manner.
There are various languages that are used for modeling:
Written Language refers to the natural language description of the model. If price of butter goes up, the quantity demanded of the butter will go down. Written language models can be used effectively to inform all of the other types of models that follow below. It often goes by the name of “qualitative” research, although we find that a bit limiting. Just a simple statement like – This model approximately reflects the behavior of people living in a dense environment …” could qualify as a written language model that seeks to shed light on the object being studied.
Icon Models refer to a pictorial representation and probably the earliest form of model making. It seeks to only qualify those contours or shapes or colors that are most interesting and relevant to the object being studied. The idea of icon models is to pictorially abstract the main elements to provide a working understanding of the object being studied.
Topological Models refer to how the variables are placed with respect to one another and thus helps in creating a classification or taxonomy of the model. Once can have logical trees, class trees, Venn diagrams, and other imaginative pictorial representation of fields to further shed light on the object being studied. In fact, pictorial representations must abide by constant scale, direction and placements. In other words, if the variables are placed on a different scale on different maps, it would be hard to draw logical conclusions by sight alone. In addition, if the placements are at different axis in different maps or have different vectors, it is hard to make comparisons and arrive at a shared consensus and a logical end result.
Arithmetic Models are what we generally fall back on most. The data is measured with an arithmetic scale. It is done via tables, equations or flow diagrams. The nice thing about arithmetic models is that you can show multiple dimensions which is not possible with other modeling languages. Hence, the robustness and the general applicability of such models are huge and thus is widely used as a key language to modeling.
Analogous Models refer to crafting explanations using the power of analogy. For example, when we talk about waves – we could be talking of light waves, radio waves, historical waves, etc. These metaphoric representations can be used to explain phenomenon, but at best, the explanatory power is nebulous, and it would be difficult to explain the variations and uncertainties between two analogous models. However, it still is used to transmit information quickly through verbal expressions like – “Similarly”, “Equivalently”, “Looks like ..” etc. In fact, extrapolation is a widely used method in modeling and we would ascertain this as part of the analogous model to a great extent. That is because we time-box the variables in the analogous model to one instance and the extrapolated model to another instance and we tie them up with mathematical equations.
Inspirational speech – stay hungry, stay foolish
This is an inspirational speech. A must see for anyone who wants to follow their heart and believe that they can make a difference. Enough said. Enjoy.
Linked Stars Blog 