Category Archives: Learning Process
Bias and Error: Human and Organizational Tradeoff
“I spent a lifetime trying to avoid my own mental biases. A.) I rub my own nose into my own mistakes. B.) I try and keep it simple and fundamental as much as I can. And, I like the engineering concept of a margin of safety. I’m a very blocking and tackling kind of thinker. I just try to avoid being stupid. I have a way of handling a lot of problems — I put them in what I call my ‘too hard pile,’ and just leave them there. I’m not trying to succeed in my ‘too hard pile.’” : Charlie Munger — 2020 CalTech Distinguished Alumni Award interview
Bias is a disproportionate weight in favor of or against an idea or thing, usually in a way that is closed-minded, prejudicial, or unfair. Biases can be innate or learned. People may develop biases for or against an individual, a group, or a belief. In science and engineering, a bias is a systematic error. Statistical bias results from an unfair sampling of a population, or from an estimation process that does not give accurate results on average.
Error refers to a outcome that is different from reality within the context of the objective function that is being pursued.
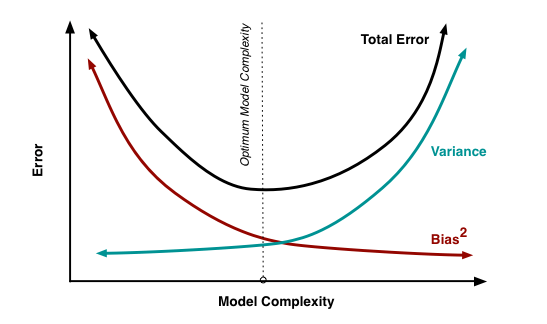
Thus, I would like to think that the Bias is a process that might lead to an Error. However, that is not always the case. There are instances where a bias might get you to an accurate or close to an accurate result. Is having a biased framework always a bad thing? That is not always the case. From an evolutionary standpoint, humans have progressed along the dimension of making rapid judgements – and much of them stemming from experience and their exposure to elements in society. Rapid judgements are typified under the System 1 judgement (Kahneman, Tversky) which allows bias and heuristic to commingle to effectively arrive at intuitive decision outcomes.
And again, the decision framework constitutes a continually active process in how humans or/and organizations execute upon their goals. It is largely an emotional response but could just as well be an automated response to a certain stimulus. However, there is a danger prevalent in System 1 thinking: it might lead one to comfortably head toward an outcome that is seemingly intuitive, but the actual result might be significantly different and that would lead to an error in the judgement. In math, you often hear the problem of induction which establishes that your understanding of a future outcome relies on the continuity of the past outcomes, and that is an errant way of thinking although it still represents a useful tool for us to advance toward solutions.
System 2 judgement emerges as another means to temper the more significant variabilities associated with System 1 thinking. System 2 thinking represents a more deliberate approach which leads to a more careful construct of rationale and thought. It is a system that slows down the decision making since it explores the logic, the assumptions, and how the framework tightly fits together to test contexts. There are a more lot more things at work wherein the person or the organization has to invest the time, focus the efforts and amplify the concentration around the problem that has to be wrestled with. This is also the process where you search for biases that might be at play and be able to minimize or remove that altogether. Thus, each of the two Systems judgement represents two different patterns of thinking: rapid, more variable and more error prone outcomes vs. slow, stable and less error prone outcomes.
So let us revisit the Bias vs. Variance tradeoff. The idea is that the more bias you bring to address a problem, there is less variance in the aggregate. That does not mean that you are accurate. It only means that there is less variance in the set of outcomes, even if all of the outcomes are materially wrong. But it limits the variance since the bias enforces a constraint in the hypotheses space leading to a smaller and closely knit set of probabilistic outcomes. If you were to remove the constraints in the hypotheses space – namely, you remove bias in the decision framework – well, you are faced with a significant number of possibilities that would result in a larger spread of outcomes. With that said, the expected value of those outcomes might actually be closer to reality, despite the variance – than a framework decided upon by applying heuristic or operating in a bias mode.
So how do we decide then? Jeff Bezos had mentioned something that I recall: some decisions are one-way street and some are two-way. In other words, there are some decisions that cannot be undone, for good or for bad. It is a wise man who is able to anticipate that early on to decide what system one needs to pursue. An organization makes a few big and important decisions, and a lot of small decisions. Identify the big ones and spend oodles of time and encourage a diverse set of input to work through those decisions at a sufficiently high level of detail. When I personally craft rolling operating models, it serves a strategic purpose that might sit on shifting sands. That is perfectly okay! But it is critical to evaluate those big decisions since the crux of the effectiveness of the strategy and its concomitant quantitative representation rests upon those big decisions. Cutting corners can lead to disaster or an unforgiving result!
I will focus on the big whale decisions now. I will assume, for the sake of expediency, that the series of small decisions, in the aggregate or by itself, will not sufficiently be large enough that it would take us over the precipice. (It is also important however to examine the possibility that a series of small decisions can lead to a more holistic unintended emergent outcome that might have a whale effect: we come across that in complexity theory that I have already touched on in a set of previous articles).
Cognitive Biases are the biggest mea culpas that one needs to worry about. Some of the more common biases are confirmation bias, attribution bias, the halo effect, the rule of anchoring, the framing of the problem, and status quo bias. There are other cognition biases at play, but the ones listed above are common in planning and execution. It is imperative that these biases be forcibly peeled off while formulating a strategy toward problem solving.
But then there are also the statistical biases that one needs to be wary of. How we select data or selection bias plays a big role in validating information. In fact, if there are underlying statistical biases, the validity of the information is questionable. Then there are other strains of statistical biases: the forecast bias which is the natural tendency to be overtly optimistic or pessimistic without any substantive evidence to support one or the other case. Sometimes how the information is presented: visually or in tabular format – can lead to sins of the error of omission and commission leading the organization and judgement down paths that are unwarranted and just plain wrong. Thus, it is important to be aware of how statistical biases come into play to sabotage your decision framework.
One of the finest illustrations of misjudgment has been laid out by Charlie Munger. Here is the excerpt link : https://fs.blog/great-talks/psychology-human-misjudgment/ He lays out a very comprehensive 25 Biases that ail decision making. Once again, stripping biases do not necessarily result in accuracy — it increases the variability of outcomes that might be clustered around a mean that might be closer to accuracy than otherwise.
Variability is Noise. We do not know a priori what the expected mean is. We are close, but not quite. There is noise or a whole set of outcomes around the mean. Viewing things closer to the ground versus higher would still create a likelihood of accepting a false hypothesis or rejecting a true one. Noise is extremely hard to sift through, but how you can sift through the noise to arrive at those signals that are determining factors, is critical to organization success. To get to this territory, we have eliminated the cognitive and statistical biases. Now is the search for the signal. What do we do then? An increase in noise impairs accuracy. To improve accuracy, you either reduce noise or figure out those indicators that signal an accurate measure.
This is where algorithmic thinking comes into play. You start establishing well tested algorithms in specific use cases and cross-validate that across a large set of experiments or scenarios. It has been proved that algorithmic tools are, in the aggregate, superior to human judgement – since it systematically can surface causal and correlative relationships. Furthermore, special tools like principal component analysis and factory analysis can incorporate a large input variable set and establish the patterns that would be impregnable for even System 2 mindset to comprehend. This will bring decision making toward the signal variants and thus fortify decision making.
The final element is to assess the time commitment required to go through all the stages. Given infinite time and resources, there is always a high likelihood of arriving at those signals that are material for sound decision making. Alas, the reality of life does not play well to that assumption! Time and resources are constraints … so one must make do with sub-optimal decision making and establish a cutoff point wherein the benefits outweigh the risks of looking for another alternative. That comes down to the realm of judgements. While George Stigler, a Nobel Laureate in Economics, introduce search optimization in fixed sequential search – a more concrete example has been illustrated in “Algorithms to Live By” by Christian & Griffiths. They suggested an holy grail response: 37% is the accurate answer. In other words, you would reach a suboptimal decision by ensuring that you have explored up to 37% of your estimated maximum effort. While the estimated maximum effort is quite ambiguous and afflicted with all of the elements of bias (cognitive and statistical), the best thinking is to be as honest as possible to assess that effort and then draw your search threshold cutoff.
An important element of leadership is about making calls. Good calls, not necessarily the best calls! Calls weighing all possible circumstances that one can, being aware of the biases, bringing in a diverse set of knowledge and opinions, falling back upon agnostic tools in statistics, and knowing when it is appropriate to have learnt enough to pull the trigger. And it is important to cascade the principles of decision making and the underlying complexity into and across the organization.
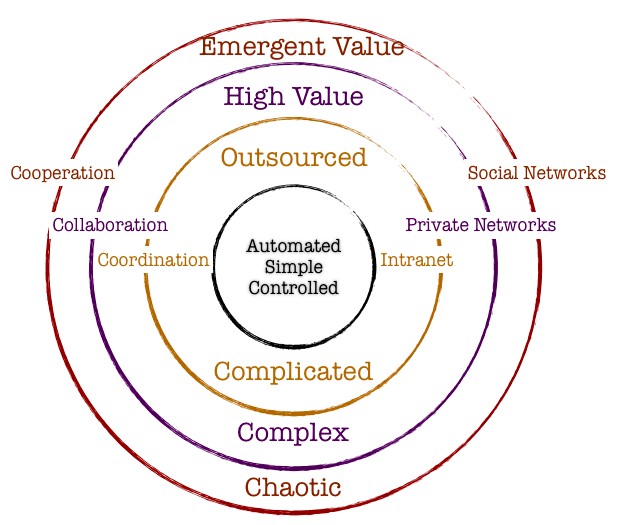
Navigating Chaos and Model Thinking
An inherent property of a chaotic system is that slight changes in initial conditions in the system result in a disproportionate change in outcome that is difficult to predict. Chaotic systems appear to create outcomes that appear to be random: they are generated by simple and non-random processes but the complexity of such systems emerge over time driven by numerous iterations of simple rules. The elements that compose chaotic systems might be few in number, but these elements work together to produce an intricate set of dynamics that amplifies the outcome and makes it hard to be predictable. These systems evolve over time, doing so according to rules and initial conditions and how the constituent elements work together.
Complex systems are characterized by emergence. The interactions between the elements of the system with its environment create new properties which influence the structural development of the system and the roles of the agents. In such systems there is self-organization characteristics that occur, and hence it is difficult to study and effect a system by studying the constituent parts that comprise it. The task becomes even more formidable when one faces the prevalent reality that most systems exhibit non-linear dynamics.
So how do we incorporate management practices in the face of chaos and complexity that is inherent in organization structure and market dynamics? It would be interesting to study this in light of the evolution of management principles in keeping with the evolution of scientific paradigms.
Newtonian Mechanics and Taylorism
Traditional organization management has been heavily influenced by Newtonian mechanics. The five key assumptions of Newtonian mechanics are:
- Reality is objective
- Systems are linear and there is a presumption that all underlying cause and effect are linear
- Knowledge is empirical and acquired through collecting and analyzing data with the focus on surfacing regularities, predictability and control
- Systems are inherently efficient. Systems almost always follows the path of least resistance
- If inputs and process is managed, the outcomes are predictable
Frederick Taylor is the father of operational research and his methods were deployed in automotive companies in the 1940’s. Workers and processes are input elements to ensure that the machine functions per expectations. There was a linearity employed in principle. Management role was that of observation and control and the system would best function under hierarchical operating principles. Mass and efficient production were the hallmarks of management goal.
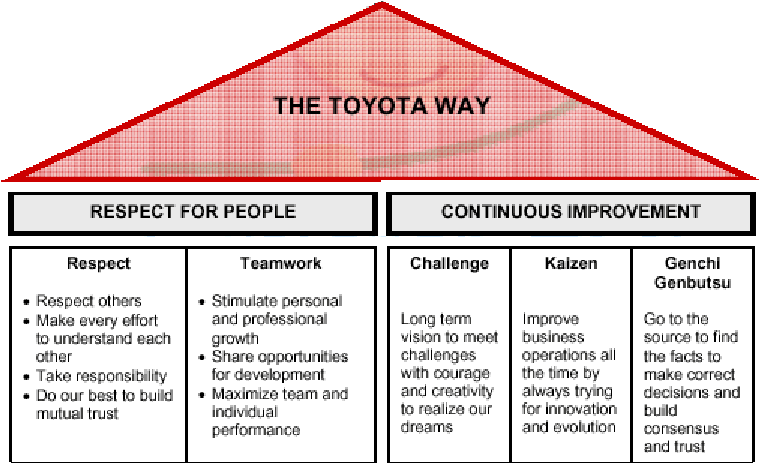
Randomness and the Toyota Way
The randomness paradigm recognized uncertainty as a pervasive constant. The various methods that Toyota Way invoked around 5W rested on the assumption that understanding the cause and effect is instrumental and this inclined management toward a more process-based deployment. Learning is introduced in this model as a dynamic variable and there is a lot of emphasis on the agents and providing them the clarity and purpose of their tasks. Efficiencies and quality are presumably driven by the rank and file and autonomous decisions are allowed. The management principle moves away from hierarchical and top-down to a more responsibility driven labor force.
Complexity and Chaos and the Nimble Organization
Increasing complexity has led to more demands on the organization. With the advent of social media and rapid information distribution and a general rise in consciousness around social impact, organizations have to balance out multiple objectives. Any small change in initial condition can lead to major outcomes: an advertising mistake can become a global PR nightmare; a word taken out of context could have huge ramifications that might immediately reflect on the stock price; an employee complaint could force management change. Increasing data and knowledge are not sufficient to ensure long-term success. In fact, there is no clear recipe to guarantee success in an age fraught with non-linearity, emergence and disequilibrium. To succeed in this environment entails the development of a learning organization that is not governed by fixed top-down rules: rather the rules are simple and the guidance is around the purpose of the system or the organization. It is best left to intellectual capital to self-organize rapidly in response to external information to adapt and make changes to ensure organization resilience and success.
Companies are dynamic non-linear adaptive systems. The elements in the system are constantly interacting between themselves and their external environment. This creates new emergent properties that are sensitive to the initial conditions. A change in purpose or strategic positioning could set a domino effect and can lead to outcomes that are not predictable. Decisions are pushed out to all levels in the organization, since the presumption is that local and diverse knowledge that spontaneously emerge in response to stimuli is a superior structure than managing for complexity in a centralized manner. Thus, methods that can generate ideas, create innovation habitats, and embrace failures as providing new opportunities to learn are best practices that companies must follow. Traditional long-term planning and forecasting is becoming a far harder exercise and practically impossible. Thus, planning is more around strategic mindset, scenario planning, allowing local rules to auto generate without direct supervision, encourage dissent and diversity, stimulate creativity and establishing clarity of purpose and broad guidelines are the hall marks of success.
Principles of Leadership in a New Age
We have already explored the fact that traditional leadership models originated in the context of mass production and efficiencies. These models are arcane in our information era today, where systems are characterized by exponential dynamism of variables, increased density of interactions, increased globalization and interconnectedness, massive information distribution at increasing rapidity, and a general toward economies driven by free will of the participants rather than a central authority.
Complexity Leadership Theory (Uhl-Bien) is a “framework for leadership that enables the learning, creative and adaptive capacity of complex adaptive systems in knowledge-producing organizations or organizational units. Since planning for the long-term is virtually impossible, Leadership has to be armed with different tool sets to steer the organization toward achieving its purpose. Leaders take on enabler role rather than controller role: empowerment supplants control. Leadership is not about focus on traits of a single leader: rather, it redirects emphasis from individual leaders to leadership as an organizational phenomenon. Leadership is a trait rather than an individual. We recognize that complex systems have lot of interacting agents – in business parlance, which might constitute labor and capital. Introducing complexity leadership is to empower all of the agents with the ability to lead their sub-units toward a common shared purpose. Different agents can become leaders in different roles as their tasks or roles morph rapidly: it is not necessarily defined by a formal appointment or knighthood in title.
Thus, complexity of our modern-day reality demands a new strategic toolset for the new leader. The most important skills would be complex seeing, complex thinking, complex knowing, complex acting, complex trusting and complex being. (Elena Osmodo, 2012)
Complex Seeing: Reality is inherently subjective. It is a page of the Heisenberg Uncertainty principle that posits that the independence between the observer and the observed is not real. If leaders are not aware of this independence, they run the risk of engaging in decisions that are fraught with bias. They will continue to perceive reality with the same lens that they have perceived reality in the past, despite the fact that undercurrents and riptides of increasingly exponential systems are tearing away their “perceived reality.” Leader have to be conscious about the tectonic shifts, reevaluate their own intentions, probe and exclude biases that could cloud the fidelity of their decisions, and engage in a continuous learning process. The ability to sift and see through this complexity sets the initial condition upon which the entire system’s efficacy and trajectory rests.
Complex Thinking: Leaders have to be cognizant of falling prey to linear simple cause and effect thinking. On the contrary, leaders have to engage in counter-intuitive thinking, brainstorming and creative thinking. In addition, encouraging dissent, debates and diversity encourage new strains of thought and ideas.
Complex Feeling: Leaders must maintain high levels of energy and be optimistic of the future. Failures are not scoffed at; rather they are simply another window for learning. Leaders have to promote positive and productive emotional interactions. The leaders are tasked to increase positive feedback loops while reducing negative feedback mechanisms to the extent possible. Entropy and attrition taxes any system as is: the leader’s job is to set up safe environment to inculcate respect through general guidelines and leading by example.
Complex Knowing: Leadership is tasked with formulating simple rules to enable learned and quicker decision making across the organization. Leaders must provide a common purpose, interconnect people with symbols and metaphors, and continually reiterate the raison d’etre of the organization. Knowing is articulating: leadership has to articulate and be humble to any new and novel challenges and counterfactuals that might arise. The leader has to establish systems of knowledge: collective learning, collaborative learning and organizational learning. Collective learning is the ability of the collective to learn from experiences drawn from the vast set of individual actors operating in the system. Collaborative learning results due to interaction of agents and clusters in the organization. Learning organization, as Senge defines it, is “where people continually expand their capacity to create the results they truly desire, where new and expansive patterns of thinking are nurtured, where collective aspirations are set free, and where people are continually learning to see the whole together.”
Complex Acting: Complex action is the ability of the leader to not only work toward benefiting the agents in his/her purview, but also to ensure that the benefits resonates to a whole which by definition is greater than the sum of the parts. Complex acting is to take specific action-oriented steps that largely reflect the values that the organization represents in its environmental context.
Complex Trusting: Decentralization requires conferring power to local agents. For decentralization to work effectively, leaders have to trust that the agents will, in the aggregate, work toward advancing the organization. The cost of managing top-down is far more than the benefits that a trust-based decentralized system would work in a dynamic environment resplendent with the novelty of chaos and complexity.
Complex Being: This is the ability of the leaser to favor and encourage communication across the organization rapidly. The leader needs to encourage relationships and inter-functional dialogue.
The role of complex leaders is to design adaptive systems that are able to cope with challenging and novel environments by establishing a few rules and encouraging agents to self-organize autonomously at local levels to solve challenges. The leader’s main role in this exercise is to set the strategic directions and the guidelines and let the organizations run.
Chaos and the tide of Entropy!
We have discussed chaos. It is rooted in the fundamental idea that small changes in the initial condition in a system can amplify the impact on the final outcome in the system. Let us now look at another sibling in systems literature – namely, the concept of entropy. We will then attempt to bridge these two concepts since they are inherent in all systems.
Entropy arises from the law of thermodynamics. Let us state all three laws:
- First law is known as the Lay of Conservation of Energy which states that energy can neither be created nor destroyed: energy can only be transferred from one form to another. Thus, if there is work in terms of energy transformation in a system, there is equivalent loss of energy transformation around the system. This fact balances the first law of thermodynamics.
- Second law of thermodynamics states that the entropy of any isolated system always increases. Entropy always increases, and rarely ever decreases. If a locker room is not tidied, entropy dictates that it will become messier and more disorderly over time. In other words, all systems that are stagnant will inviolably run against entropy which would lead to its undoing over time. Over time the state of disorganization increases. While energy cannot be created or destroyed, as per the First Law, it certainly can change from useful energy to less useful energy.
- Third law establishes that the entropy of a system approaches a constant value as the temperature approaches absolute zero. Thus, the entropy of a pure crystalline substance at absolute zero temperature is zero. However, if there is any imperfection that resides in the crystalline structure, there will be some entropy that will act upon it.
Entropy refers to a measure of disorganization. Thus people in a crowd that is widely spread out across a large stadium has high entropy whereas it would constitute low entropy if people are all huddled in one corner of the stadium. Entropy is the quantitative measure of the process – namely, how much energy has been spent from being localized to being diffused in a system. Entropy is enabled by motion or interaction of elements in a system, but is actualized by the process of interaction. All particles work toward spontaneously dissipating their energy if they are not curtailed from doing so. In other words, there is an inherent will, philosophically speaking, of a system to dissipate energy and that process of dissipation is entropy. However, it makes no effort to figure out how quickly entropy kicks into gear – it is this fact that makes it difficult to predict the overall state of the system.
Chaos, as we have already discussed, makes systems unpredictable because of perturbations in the initial state. Entropy is the dissipation of energy in the system, but there is no standard way of knowing the parameter of how quickly entropy would set in. There are thus two very interesting elements in systems that almost work simultaneously to ensure that predictability of systems become harder.
Another way of looking at entropy is to view this as a tax that the system charges us when it goes to work on our behalf. If we are purposefully calibrating a system to meet a certain purpose, there is inevitably a corresponding usage of energy or dissipation of energy otherwise known as entropy that is working in parallel. A common example that we are familiar with is mass industrialization initiatives. Mass industrialization has impacts on environment, disease, resource depletion, and a general decay of life in some form. If entropy as we understand it is an irreversible phenomenon, then there is virtually nothing that can be done to eliminate it. It is a permanent tax of varying magnitude in the system.
Humans have since early times have tried to formulate a working framework of the world around them. To do that, they have crafted various models and drawn upon different analogies to lend credence to one way of thinking over another. Either way, they have been left best to wrestle with approximations: approximations associated with their understanding of the initial conditions, approximations on model mechanics, approximations on the tax that the system inevitably charges, and the approximate distribution of potential outcomes. Despite valiant efforts to reduce the framework to physical versus behavioral phenomena, their final task of creating or developing a predictable system has not worked. While physical laws of nature describe physical phenomena, the behavioral laws describe non-deterministic phenomena. If linear equations are used as tools to understand the physical laws following the principles of classical Newtonian mechanics, the non-linear observations marred any consistent and comprehensive framework for clear understanding. Entropy reaches out toward an irreversible thermal death: there is an inherent fatalism associated with the Second Law of Thermodynamics. However, if that is presumed to be the case, how is it that human evolution has jumped across multiple chasms and have evolved to what it is today? If indeed entropy is the tax, one could argue that chaos with its bounded but amplified mechanics have allowed the human race to continue.
Let us now deliberate on this observation of Richard Feynmann, a Nobel Laurate in physics – “So we now have to talk about what we mean by disorder and what we mean by order. … Suppose we divide the space into little volume elements. If we have black and white molecules, how many ways could we distribute them among the volume elements so that white is on one side and black is on the other? On the other hand, how many ways could we distribute them with no restriction on which goes where? Clearly, there are many more ways to arrange them in the latter case.
We measure “disorder” by the number of ways that the insides can be arranged, so that from the outside it looks the same. The logarithm of that number of ways is the entropy. The number of ways in the separated case is less, so the entropy is less, or the “disorder” is less.” It is commonly also alluded to as the distinction between microstates and macrostates. Essentially, it says that there could be innumerable microstates although from an outsider looking in – there is only one microstate. The number of microstates hints at the system having more entropy.
In a different way, we ran across this wonderful example: A professor distributes chocolates to students in the class. He has 35 students but he distributes 25 chocolates. He throws those chocolates to the students and some students might have more than others. The students do not know that the professor had only 25 chocolates: they have presumed that there were 35 chocolates. So the end result is that the students are disconcerted because they perceive that the other students have more chocolates than they have distributed but the system as a whole shows that there are only 25 chocolates. Regardless of all of the ways that the 25 chocolates are configured among the students, the microstate is stable.
So what is Feynmann and the chocolate example suggesting for our purpose of understanding the impact of entropy on systems: Our understanding is that the reconfiguration or the potential permutations of elements in the system that reflect the various microstates hint at higher entropy but in reality has no impact on the microstate per se except that the microstate has inherently higher entropy. Does this mean that the macrostate thus has a shorter life-span? Does this mean that the microstate is inherently more unstable? Could this mean an exponential decay factor in that state? The answer to all of the above questions is not always. Entropy is a physical phenomenon but to abstract this out to enable a study of organic systems that represent super complex macrostates and arrive at some predictable pattern of decay is a bridge too far! If we were to strictly follow the precepts of the Second Law and just for a moment forget about Chaos, one could surmise that evolution is not a measure of progress, it is simply a reconfiguration.
Theodosius Dobzhansky, a well known physicist, says: “Seen in retrospect, evolution as a whole doubtless had a general direction, from simple to complex, from dependence on to relative independence of the environment, to greater and greater autonomy of individuals, greater and greater development of sense organs and nervous systems conveying and processing information about the state of the organism’s surroundings, and finally greater and greater consciousness. You can call this direction progress or by some other name.”
Harold Mosowitz says “Life is organization. From prokaryotic cells, eukaryotic cells, tissues and organs, to plants and animals, families, communities, ecosystems, and living planets, life is organization, at every scale. The evolution of life is the increase of biological organization, if it is anything. Clearly, if life originates and makes evolutionary progress without organizing input somehow supplied, then something has organized itself. Logical entropy in a closed system has decreased. This is the violation that people are getting at, when they say that life violates the second law of thermodynamics. This violation, the decrease of logical entropy in a closed system, must happen continually in the Darwinian account of evolutionary progress.”
Entropy occurs in all systems. That is an indisputable fact. However, if we start defining boundaries, then we are prone to see that these bounded systems decay faster. However, if we open up the system to leave it unbounded, then there are a lot of other forces that come into play that is tantamount to some net progress. While it might be true that energy balances out, what we miss as social scientists or model builders or avid students of systems – we miss out on indices that reflect on leaps in quality and resilience and a horde of other factors that stabilizes the system despite the constant and ominous presence of entropy’s inner workings.
Chaos as a system: New Framework
Chaos is not an unordered phenomenon. There is a certain homeostatic mechanism at play that forces a system that might have inherent characteristics of a “chaotic” process to converge to some sort of stability with respect to predictability and parallelism. Our understanding of order which is deemed to be opposite of chaos is the fact that there is a shared consensus that the system will behave in an expected manner. Hence, we often allude to systems as being “balanced” or “stable” or “in order” to spotlight these systems. However, it is also becoming common knowledge in the science of chaos that slight changes in initial conditions in a system can emit variability in the final output that might not be predictable. So how does one straddle order and chaos in an observed system, and what implications does this process have on ongoing study of such systems?
Chaotic systems can be considered to have a highly complex order. It might require the tools of pure mathematics and extreme computational power to understand such systems. These tools have invariably provided some insights into chaotic systems by visually representing outputs as re-occurrences of a distribution of outputs related to a given set of inputs. Another interesting tie up in this model is the existence of entropy, that variable that taxes a system and diminishes the impact on expected outputs. Any system acts like a living organism: it requires oodles of resources to survive and a well-established set of rules to govern its internal mechanism driving the vector of its movement. Suddenly, what emerges is the fact that chaotic systems display some order while subject to an inherent mechanism that softens its impact over time. Most approaches to studying complex and chaotic systems involve understanding graphical plots of fractal nature, and bifurcation diagrams. These models illustrate very complex re occurrences of outputs directly related to inputs. Hence, complex order occurs from chaotic systems.
A case in point would be the relation of a population parameter in the context to its immediate environment. It is argued that a population in an environment will maintain a certain number and there would be some external forces that will actively work to ensure that the population will maintain at that standard number. It is a very Malthusian analytic, but what is interesting is that there could be some new and meaningful influences on the number that might increase the scale. In our current meaning, a change in technology or ingenuity could significantly alter the natural homeostatic number. The fact remains that forces are always at work on a system. Some systems are autonomic – it self-organizes and corrects itself toward some stable convergence. Other systems are not autonomic and once can only resort to the laws of probability to get some insight into the possible outputs – but never to a point where there is a certainty in predictive prowess.
Organizations have a lot of interacting variables at play at any given moment. In order to influence the organization behavior or/and direction, policies might be formulated to bring about the desirable results. However, these nudges toward setting off the organization in the right direction might also lead to unexpected results. The aim is to foresee some of these unexpected results and mollify the adverse consequences while, in parallel, encourage the system to maximize the benefits. So how does one effect such changes?
It all starts with building out an operating framework. There needs to be a clarity around goals and what the ultimate purpose of the system is. Thus there are few objectives that bind the framework.
- Clarity around goals and the timing around achieving these goals. If there is no established time parameter, then the system might jump across various states over time and it would be difficult to establish an outcome.
- Evaluate all of the internal and external factors that might operate in the framework that would impact the success of organizational mandates and direction. Identify stasis or potential for stasis early since that mental model could stem the progress toward a desirable impact.
- Apply toll gates strategically to evaluate if the system is proceeding along the lines of expectation, and any early aberrations are evaluated and the rules are tweaked to get the system to track on a desirable trajectory.
- Develop islands of learning across the path and engage the right talent and other parameters to force adaptive learning and therefore a more autonomic direction to the system.
- Bind the agents and actors in the organization to a shared sense of purpose within the parameter of time.
- Introduce diversity into the framework early in the process. The engagement of diversity allows the system to modulate around a harmonic mean.
- Finally, maintain a well document knowledge base such that the accretive learning that results due to changes in the organization become springboard for new initiatives that reduces the costs of potential failures or latency in execution.
- Encouraging the leadership to ensure that the vector is pointed toward the right direction at any given time.
Once a framework and the engagement rules are drawn out, it is necessary to rely on the natural velocity and self-organization of purposeful agents to move the agenda forward, hopefully with little or no intervention. A mechanism of feedback loops along the way would guide the efficacy of the direction of the system. The implications is that the strategy and the operations must be aligned and reevaluated and positive behavior is encouraged to ensure that the systems meets its objective.
However, as noted above, entropy is a dynamic that often threatens to derail the system objective. There will be external or internal forces constantly at work to undermine system velocity. The operating framework needs to anticipate that real possibility and pre-empt that with rules or introduction of specific capital to dematerialize these occurrences. Stasis is an active agent that can work against the system dynamic. Stasis is the inclination of agents or behaviors that anchors the system to some status quo – we have to be mindful that change might not be embraced and if there are resistors to that change, the dynamic of organizational change can be invariably impacted. It will take a lot more to get something done than otherwise needed. Identifying stasis and agents of stasis is a foundational element
While the above is one example of how to manage organizations in the shadows of the properties of how chaotic systems behave, another example would be the formulation of strategy of the organization in responses to external forces. How do we apply our learnings in chaos to deal with the challenges of competitive markets by aligning the internal organization to external factors? One of the key insights that chaos surfaces is that it is nigh impossible for one to fully anticipate all of the external variables, and leaving the system to dynamically adapt organically to external dynamics would allow the organization to thrive. To thrive in this environment is to provide the organization to rapidly change outside of the traditional hierarchical expectations: when organizations are unable to make those rapid changes or make strategic bets in response to the external systems, then the execution value of the organization diminishes.
Margaret Wheatley in her book Leadership and the New Science: Discovering Order in a Chaotic World Revised says, “Organizations lack this kind of faith, faith that they can accomplish their purposes in various ways and that they do best when they focus on direction and vision, letting transient forms emerge and disappear. We seem fixated on structures…and organizations, or we who create them, survive only because we build crafty and smart—smart enough to defend ourselves from the natural forces of destruction. Karl Weick, an organizational theorist, believes that “business strategies should be “just in time…supported by more investment in general knowledge, a large skill repertoire, the ability to do a quick study, trust in intuitions, and sophistication in cutting losses.”
We can expand the notion of a chaos in a system to embrace the bigger challenges associated with environment, globalization, and the advent of disruptive technologies.
One of the key challenges to globalization is how policy makers would balance that out against potential social disintegration. As policies emerge to acknowledge the benefits and the necessity to integrate with a new and dynamic global order, the corresponding impact to local institutions can vary and might even lead to some deleterious impact on those institutions. Policies have to encourage flexibility in local institutional capability and that might mean increased investments in infrastructure, creating a diverse knowledge base, establishing rules that govern free but fair trading practices, and encouraging the mobility of capital across borders. The grand challenges of globalization is weighed upon by government and private entities that scurry to create that continual balance to ensure that the local systems survive and flourish within the context of the larger framework. The boundaries of the system are larger and incorporates many more agents which effectively leads to the real possibility of systems that are difficult to be controlled via a hierarchical or centralized body politic Decision making is thus pushed out to the agents and actors but these work under a larger set of rules. Rigidity in rules and governance can amplify failures in this process.
Related to the realities of globalization is the advent of the growth in exponential technologies. Technologies with extreme computational power is integrating and create robust communication networks within and outside of the system: the system herein could represent nation-states or companies or industrialization initiatives. Will the exponential technologies diffuse across larger scales quickly and will the corresponding increase in adoption of new technologies change the future of the human condition? There are fears that new technologies would displace large groups of economic participants who are not immediately equipped to incorporate and feed those technologies into the future: that might be on account of disparity in education and wealth, institutional policies, and the availability of opportunities. Since technologies are exponential, we get a performance curve that is difficult for us to understand. In general, we tend to think linearly and this frailty in our thinking removes us from the path to the future sooner than later. What makes this difficult is that the exponential impact is occurring across various sciences and no one body can effectively fathom the impact and the direction. Bill Gates says it well “We always overestimate the change that will occur in the next two years and underestimate the change that will occur in the next ten. Don’t let yourself be lulled into inaction.” Does chaos theory and complexity science arm us with a differentiated tool set than the traditional toolset of strategy roadmaps and product maps? If society is being carried by the intractable and power of the exponent in advances in technology, than a linear map might not serve to provide the right framework to develop strategies for success in the long-term. Rather, a more collaborative and transparent roadmap to encourage the integration of thoughts and models among the actors who are adapting and adjusting dynamically by the sheer force of will would perhaps be an alternative and practical approach in the new era.
Lately there has been a lot of discussion around climate change. It has been argued, with good reason and empirical evidence, that environment can be adversely impacted on account of mass industrialization, increase in population, resource availability issues, the inability of the market system to incorporate the cost of spillover effects, the adverse impact of moral hazard and the theory of the commons, etc. While there are demurrers who contest the long-term climate change issues, the train seems to have already left the station! The facts do clearly reflect that the climate will be impacted. Skeptics might argue that science has not yet developed a precise predictive model of the weather system two weeks out, and it is foolhardy to conclude a dystopian future on climate fifty years out. However, the alternative argument is that our inability to exercise to explain the near-term effects of weather changes and turbulence does not negate the existence of climate change due to the accretion of greenhouse impact. Boiling a pot of water will not necessarily gives us an understanding of all of the convection currents involved among the water molecules, but it certainly does not shy away from the fact that the water will heat up.
History of Chaos
| Chaos is inherent in all compounded things. Strive on with diligence! –Buddha |
Scientific theories are characterized by the fact that they are open to refutation. To create a scientific model, there are three successive steps that one follows: observe the phenomenon, translate that into equations, and then solve the equations.
One of the early philosophers of science, Karl Popper (1902-1994) discussed this at great length in his book – The Logic of Scientific Discovery. He distinguishes scientific theories from metaphysical or mythological assertions. His main theses is that a scientific theory must be open to falsification: it has to be reproducible separately and yet one can gather data points that might refute the fundamental elements of theory. Developing a scientific theory in a manner that can be falsified by observations would result in new and more stable theories over time. Theories can be rejected in favor of a rival theory or a calibration of the theory in keeping with the new set of observations and outcomes that the theories posit. Until Popper’s time and even after, social sciences have tried to work on a framework that would allow the construction of models that would formulate some predictive laws that govern social dynamics. In his book, Poverty of Historicism, Popper maintained that such an endeavor is not fruitful since it does not take into consideration the myriad of minor elements that interact closely with one another in a meaningful way. Hence, he has touched indirectly on the concept of chaos and complexity and how it touches the scientific method. We will now journey into the past and through the present to understand the genesis of the theory and how it has been channelized by leading scientists and philosophers to decipher a framework for study society and nature.
As we have already discussed, one of the main pillars of Science is determinism: the probability of prediction. It holds that every event is determined by natural laws. Nothing can happen without an unbroken chain of causes that can be traced all the way back to an initial condition. The deterministic nature of science goes all the way back to Aristotelian times. Interestingly, Aristotle argued that there is some degree of indeterminism and he relegated this to chance or accidents. Chance is a character that makes its presence felt in every plot in the human and natural condition. Aristotle wrote that “we do not have knowledge of a thing until we have grasped its why, that is to say, its cause.” He goes on to illustrate his idea in greater detail – namely, that the final outcome that we see in a system is on account of four kinds of influencers: Matter, Form, Agent and Purpose.
Matter is what constitutes the outcome. For a chair it might be wood. For a statue, it might be marble. The outcome is determined by what constitutes the outcome.
Form refers to the shape of the outcome. Thus, a carpenter or a sculptor would have a pre-conceived notion of the shape of the outcome and they would design toward that artifact.
Agent refers to the efficient cause or the act of producing the outcome. Carpentry or masonry skills would be important to shape the final outcome.
Finally, the outcome itself must serve a purpose on its own. For a chair, it might be something to sit on, for a statue it might be something to be marveled at.
However, Aristotle also admits that luck and chance can play an important role that do not fit the causal framework in its own right. Some things do happen by chance or luck. Chance is a rare event, it is a random event and it is typically brought out by some purposeful action or by nature.
We had briefly discussed the Laplace demon and he summarized this wonderfully: “We ought then to consider the resent state of the universe as the effect of its previous state and as the cause of that which is to follow. An intelligence that, at a given instant, could comprehend all the forces by which nature is animated and the respective situation of the beings that make it up if moreover it were vast enough to submit these data to analysis, would encompass in the same formula the movements of the greatest bodies of the universe and those of the lightest atoms. For such an intelligence nothing would be uncertain, and the future, like the past, would be open to its eyes.” He thus admits to the fact that we lack the vast intelligence and we are forced to use probabilities in order to get a sense of understanding of dynamical systems.
It was Maxwell in his pivotal book “Matter and Motion” published in 1876 lay the groundwork of chaos theory.
“There is a maxim which is often quoted, that “the same causes will always produce the same effects.’ To make this maxim intelligible we must define what we mean by the same causes and the same effects, since it is manifest that no event ever happens more than once, so that the causes and effects cannot be the same in all respects. There is another maxim which must not be confounded with that quoted at the beginning of this article, which asserts “That like causes produce like effects.” This is only true when small variations in the initial circumstances produce only small variations in the final state of the system. In a great many physical phenomena this condition is satisfied: but there are other cases in which a small initial variation may produce a great change in the final state of the system, as when the displacement of the points cause a railway train to run into another instead of keeping its proper course.” What is interesting however in the above quote is that Maxwell seems to go with the notion that in a great many cases there is no sensitivity to initial conditions.
In the 1890’s Henri Poincare was the first exponent of chaos theory. He says “it may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible.” This was a far cry from the Newtonian world which sought order on how the solar system worked. Newton’s model was posted on the basis of the interaction between just two bodies. What would then happen if three bodies or N bodies were introduced into the model. This led to the rise of the Three Body Problem which led to Poincare embracing the notion that this problem could not be solved and can be tackled by approximate numerical techniques. Solving this resulted in solutions that were so tangled that is was difficult to not only draw them, it was near impossible to derive equations to fit the results. In addition, Poincare also discovered that if the three bodies started from slightly different initial positions, the orbits would trace out different paths. This led to Poincare forever being designated as the Father of Chaos Theory since he laid the groundwork on the most important element in chaos theory which is the sensitivity to initial dependence.
In the early 1960’s, the first true experimenter in chaos was a meteorologist named Edward Lorenz. He was working on a problem in weather prediction and he set up a system with twelve equations to model the weather. He set the initial conditions and the computer was left to predict what the weather might be. Upon revisiting this sequence later on, he inadvertently and by sheer accident, decided to run the sequence again in the middle and he noticed that the outcome was significantly different. The imminent question that followed was why the outcome was so different than the original. He traced this back to the initial condition wherein he noted that the initial input was different with respect to the decimal places. The system incorporated the all of the decimal places rather than the first three. (He had originally input the number .506 and he had concatenated the number from .506127). He would have expected that this thin variation in input would have created a sequence close to the original sequence but that was not to be: it was distinctly and hugely different. This effect became known as the Butterfly effect which is often substituted for Chaos Theory. Ian Stewart in his book, Does God Play Dice? The Mathematics of Chaos, describes this visually as follows:
“The flapping of a single butterfly’s wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month’s time, a tornado that would have devastated the Indonesian cost doesn’t happen. Or maybe one that wasn’t going to happen, does.”
Lorenz thus argued that it would be impossible to predict the weather accurately. However, he reduced his experiment to fewer set of equations and took upon observations of how small change in initial conditions affect predictability of smaller systems. He found a parallel – namely, that changes in initial conditions tends to render the final outcome of a system to be inaccurate. As he looked at alternative systems, he found a strange pattern that emerged – namely, that the system always represented a double spiral – the system never settled down to a single point but they never repeated its trajectory. It was a path breaking discovery that led to further advancement in the science of chaos in later years.
Years later, Robert May investigated how this impacts population. He established an equation that reflected a population growth and initialized the equation with a parameter for growth rate value. (The growth rate was initialized to 2.7). May found that as he increased the parameter value, the population grew which was expected. However, once he passed the 3.0 growth value, he noticed that equation would not settle down to a single population but branch out to two different values over time. If he raised the initial value more, the bifurcation or branching of the population would be twice as much or four different values. If he continued to increase the parameter, the lines continue to double until chaos appeared and it became hard to make point predictions.
There was another innate discovery that occurred through the experiment. When one visually looks at the bifurcation, one tends to see similarity between the small and large branches. This self-similarity became an important part of the development of chaos theory.
Benoit Mandelbrot started to study this self-similarity pattern in chaos. He was an economist and he applied mathematical equations to predict fluctuations in cotton prices. He noted that particular price changes were not predictable but there were certain patterns that were repeated and the degree of variation in prices had remained largely constant. This is suggestive of the fact that one might, upon preliminary reading of chaos, arrive at the notion that if weather cannot be predictable, then how can we predict climate many years out. On the contrary, Mandelbrot’s experiments seem to suggest that short time horizons are difficult to predict that long time horizon impact since systems tend to settle into some patterns that is reflecting of smaller patterns across periods. This led to the development of the concept of fractal dimensions, namely that sub-systems develop a symmetry to a larger system.
Feigenbaum was a scientist who became interested in how quickly bifurcations occur. He discovered that regardless of the scale of the system, the came at a constant rate of 4.669. If you reduce or enlarge the scale by that constant, you would see the mechanics at work which would lead to an equivalence in self-similarity. He applied this to a number of models and the same scaling constant took effect. Feigenbaum had established, for the first time, a universal constant around chaos theory. This was important because finding a constant in the realm of chaos theory was suggestive of the fact that chaos was an ordered process, not a random one.
Sir James Lighthill gave a lecture and in that he made an astute observation –
“We are all deeply conscious today that the enthusiasm of our forebears for the marvelous achievements of Newtonian mechanics led them to make generalizations in this area of predictability which, indeed, we may have generally tended to believe before 1960, but which we now recognize were false. We collectively wish to apologize for having misled the general educated public by spreading ideas about determinism of systems satisfying Newton’s laws of motion that, after 1960, were to be proved incorrect.”
Network Theory and Network Effects
Complexity theory needs to be coupled with network theory to get a more comprehensive grasp of the underlying paradigms that govern the outcomes and morphology of emergent systems. In order for us to understand the concept of network effects which is commonly used to understand platform economics or ecosystem value due to positive network externalities, we would like to take a few steps back and appreciate the fundamental theory of networks. This understanding will not only help us to understand complexity and its emergent properties at a low level but also inform us of the impact of this knowledge on how network effects can be shaped to impact outcomes in an intentional manner.
There are first-order conditions that must be met to gauge whether the subject of the observation is a network. Firstly, networks are all about connectivity within and between systems. Understanding the components that bind the system would be helpful. However, do keep in mind that complexity systems (CPS and CAS) might have emergent properties due to the association and connectivity of the network that might not be fully explained by network theory. All the same, understanding networking theory is a building block to understanding emergent systems and the outcome of its structure on addressing niche and macro challenges in society.
Networks operates spatially in a different space and that has been intentionally done to allow some simplification and subsequent generalization of principles. The geometry of network is called network topology. It is a 2D perspective of connectivity.
Networks are subject to constraints (physical resources, governance constraint, temporal constraints, channel capacity, absorption and diffusion of information, distribution constraint) that might be internal (originated by the system) or external (originated in the environment that the network operates in).
Finally, there is an inherent non-linearity impact in networks. As nodes increase linearly, connections will increase exponentially but might be subject to constraints. The constraints might define how the network structure might morph and how information and signals might be processed differently.
Graph theory is the most widely used tool to study networks. It consists of four parts: vertices which represent an element in the network, edges refer to relationship between nodes which we call links, directionality which refers to how the information is passed ( is it random and bi-directional or follows specific rules and unidirectional), channels that refer to bandwidth that carry information, and finally the boundary which establishes specificity around network operations. A graph can be weighted – namely, a number can be assigned to each length to reflect the degree of interaction or the strength of resources or the proximity of the nodes or the ordering of discernible clusters.
The central concept of network theory thus revolves around connectivity between nodes and how non-linear emergence occurs. A node can have multiple connections with other node/nodes and we can weight the node accordingly. In addition, the purpose of networks is to pass information in the most efficient manner possible which relays into the concept of a geodesic which is either the shortest path between two nodes that must work together to achieve a purpose or the least number of leaps through links that information must negotiate between the nodes in the network.
Technically, you look for the longest path in the network and that constitutes the diameter while you calculate the average path length by examining the shortest path between nodes, adding all of those paths up and then dividing by the number of pairs. Significance of understanding the geodesic allows an understanding of the size of the network and throughput power that the network is capable of.
Nodes are the atomic elements in the network. It is presumed that its degree of significance is related to greater number of connections. There are other factors that are important considerations: how adjacent or close are the nodes to one another, does some nodes have authority or remarkable influence on others, are nodes positioned to be a connector between other nodes, and how capable are the nodes in absorbing, processing and diffusing the information across the links or channels. How difficult is it for the agents or nodes in the network to make connections? It is presumed that if the density of the network is increased, then we create a propensity in the overall network system to increase the potential for increased connectivity.
As discussed previously, our understanding of the network is deeper once we understand the elements well. The structure or network topology is represented by the graph and then we must understand size of network and the patterns that are manifested in the visual depiction of the network. Patterns, for our purposes, might refer to clusters of nodes that are tribal or share geographical proximity that self-organize and thus influence the structure of the network. We will introduce a new term homophily where agents connect with those like themselves. This attribute presumably allows less resources needed to process information and diffuse outcomes within the cluster. Most networks have a cluster bias: in other words, there are areas where there is increased activity or increased homogeneity in attributes or some form of metric that enshrines a group of agents under one specific set of values or activities. Understanding the distribution of cluster and the cluster bias makes it easier to influence how to propagate or even dismantle the network. This leads to an interesting question: Can a network that emerges spontaneously from the informal connectedness between agents be subjected to some high dominance coefficient – namely, could there be nodes or links that might exercise significant weight on the network?
The network has to align to its environment. The environment can place constraints on the network. In some instances, the agents have to figure out how to overcome or optimize their purpose in the context of the presence of the environmental constraints. There is literature that suggests the existence of random networks which might be an initial state, but it is widely agreed that these random networks self-organize around their purpose and their interaction with its environment. Network theory assigns a number to the degree of distribution which means that all or most nodes have an equivalent degree of connectivity and there is no skewed influence being weighed on the network by a node or a cluster. Low numbers assigned to the degree of distribution suggest a network that is very democratic versus high number that suggests centralization. To get a more practical sense, a mid-range number assigned to a network constitutes a decentralized network which has close affinities and not fully random. We have heard of the six degrees of separation and that linkage or affinity is most closely tied to a mid-number assignment to the network.
We are now getting into discussions on scale and binding this with network theory. Metcalfe’s law states that the value of a network grows as a square of the number of the nodes in the network. More people join the network, the more valuable the network. Essentially, there is a feedback loop that is created, and this feedback loop can kindle a network to grow exponentially. There are two other topics – Contagion and Resilience. Contagion refers to the ability of the agents to diffuse information. This information can grow the network or dismantle it. Resilience refers to how the network is organized to preserve its structure. As you can imagine, they have huge implications that we see. How do certain ideas proliferate over others, how does it cluster and create sub-networks which might grow to become large independent networks and how it creates natural defense mechanisms against self-immolation and destruction?
Network effect is commonly known as externalities in economics. It is an effect that is external to the transaction but influences the transaction. It is the incremental benefit gained by an existing user for each new user that joins the network. There are two types of network effects: Direct network effects and Indirect network effect. Direct network effects are same side effects. The value of a service goes up as the number of users goes up. For example, if more people have phones, it is useful for you to have a phone. The entire value proposition is one-sided. Indirect networks effects are multi-sided. It lends itself to our current thinking around platforms and why smart platforms can exponentially increase the network. The value of the service increases for one user group when a new user group joins the network. Take for example the relationship between credit card banks, merchants and consumers. There are three user groups, and each gather different value from the network of agents that have different roles. If more consumers use credit cards to buy, more merchants will sign up for the credit cards, and as more merchants sign up – more consumers will sign up with the bank to get more credit cards. This would be an example of a multi-sided platform that inherently has multi-sided network effects. The platform inherently gains significant power such that it becomes more valuable for participants in the system to join the network despite the incremental costs associated with joining the network. Platforms that are built upon effective multi-sided network effects grow quickly and are generally sustainable. Having said that, it could be just as easy that a few dominant bad actors in the network can dismantle and unravel the network completely. We often hear of the tipping point: namely, that once the platform reaches a critical mass of users, it would be difficult to dismantle it. That would certainly be true if the agents and services are, in the aggregate, distributed fairly across the network: but it is also possible that new networks creating even more multi-sided network effects could displace an entrenched network. Hence, it is critical that platform owners manage the quality of content and users and continue to look for more opportunities to introduce more user groups to entrench and yet exponentially grow the network.
Winner Take All Strategy
Being the first to cross the finish line makes you a winner in only one phase of life. It’s what you do after you cross the line that really counts.
– Ralph Boston
Does winner-take-all strategy apply outside the boundaries of a complex system? Let us put it another way. If one were to pursue a winner-take-all strategy, then does this willful strategic move not bind them to the constraints of complexity theory? Will the net gains accumulate at a pace over time far greater than the corresponding entropy that might be a by-product of such a strategy? Does natural selection exhibit a winner-take-all strategy over time and ought we then to regard that winning combination to spur our decisions around crafting such strategies? Are we fated in the long run to arrive at a world where there will be a very few winners in all niches and what would that mean? How does that surmise with our good intentions of creating equal opportunities and a fair distribution of access to resources to a wider swath of the population? In other words, is a winner take all a deterministic fact and does all our trivial actions to counter that constitute love’s labor lost?
Natural selection is a mechanism for evolution. It explains how populations or species evolve or modify over time in such a manner that it becomes better suited to their environments. Recall the discussion on managing scale in the earlier chapter where we discussed briefly about aligning internal complexity to external complexity. Natural selection is how it plays out at a biological level. Essentially natural selection posits that living organisms have inherited traits that help them to survive and procreate. These organisms will largely leave more offspring than their peers since the presumption is that these organisms will carry key traits that will survive the vagaries of external complexity and environment (predators, resource scarcity, climate change, etc.) Since these traits are passed on to the next generate, these traits will become more common until such time that the traits are dominant over generations, if the environment has not been punctuated with massive changes. These organisms with these dominant traits will have adapted to their environment. Natural selection does not necessarily suggest that what is good for one is good for the collective species.
An example that was shared by Robert Frank in his book “The Darwin Economy” was the case of large antlers of the bull elk. These antlers developed as an instrument for attracting mates rather than warding off predators. Big antlers would suggest a greater likelihood of the bull elk to marginalize the elks with smaller antlers. Over time, the bull elks with small antlers would die off since they would not be able to produce offspring and pass their traits. Thus, the bull elks would largely comprise of those elks with large antlers. However, the flip side is that large antlers compromise mobility and thus are more likely to be attacked by predators. Although the individual elk with large antler might succeed to stay around over time, it is also true that the compromised mobility associated with large antlers would overall hurt the propagation of the species as a collective group. We will return to this very important concept later. The interests of individual animals were often profoundly in conflict with the broader interests of their own species. Corresponding to the development of the natural selection mechanism is the introduction of the concept of the “survival of the fittest” which was introduced by Herbert Spencer. One often uses natural selection and survival of the fittest interchangeable and that is plain wrong. Natural selection never claims that the species that will emerge is the strongest, the fastest, the largest, etc.: it simply claims that the species will be the fittest, namely it will evolve in a manner best suited for the environment in which it resides. Put it another way: survival of the most sympathetic is perhaps more applicable. Organisms that are more sympathetic and caring and work in harmony with the exigencies of an environment that is largely outside of their control would likely succeed and thrive.
We will digress into the world of business. A common conception that is widely discussed is that businesses must position toward a winner-take-all strategy – especially, in industries that have very high entry costs. Once these businesses entrench themselves in the space, the next immediate initiative would be to literally launch a full-frontal assault involving huge investments to capture the mind and the wallet of the customer. Peter Thiel says – Competition is for losers. If you want to create and capture lasting value, look to build a monopoly.” Once that is built, it would be hard to displace!
Scaling the organization intentionally is key to long-term success. There are a number of factors that contribute toward developing scale and thus establishing a strong footing in the particular markets. We are listing some of the key factors below:
- Barriers to entry: Some organizations have natural cost prohibitive barriers to entry like utility companies or automobile plants. They require large investments. On the other hand, organizations can themselves influence and erect huge barriers to entry even though the barriers did not exist. Organizations would massively invest in infrastructure, distribution, customer acquisition and retention, brand and public relations. Organizations that are able to rapidly do this at a massive scale would be the ones that is expected to exercise their leverage over a big consumption base well into the future.
- Multi-sided platform impacts: The value of information across multiple subsystems: company, supplier, customer, government increases disproportionately as it expands. We had earlier noted that if cities expand by 100%, then there is increasing innovating and goods that generate 115% -the concept of super-linear scaling. As more nodes are introduced into the system and a better infrastructure is created to support communication and exchange between the nodes, the more entrenched the business becomes. And interestingly, the business grows at a sub-linear scale – namely, it consumes less and less resources in proportion to its growth. Hence, we see the large unicorn valuation among companies where investors and market makers place calculated bets on investments of colossal magnitudes. The magnitude of such investments is relatively a recent event, and this is largely driven by the advances in technology that connect all stakeholders.
- Investment in learning: To manage scale is to also be selective of information that a system receives and how the information is processed internally. In addition, how is this information relayed to the external system or environment. This requires massive investment in areas like machine learning, artificial intelligence, big data, enabling increased computational power, development of new learning algorithms, etc. This means that organizations have to align infrastructure and capability while also working with external environments through public relations, lobbying groups and policymakers to chaperone a comprehensive and a very complex hard-to-replicate learning organism.
- Investment in brand: Brand personifies the value attributes of an organization. One connects brand to customer experience and perception of the organization’s product. To manage scale and grow, organizations must invest in brand: to capture increased mindshare of the consumer. In complexity science terms, the internal systems are shaped to emit powerful signals to the external environment and urge a response. Brand and learning work together to allow a harmonic growth of an internal system in the context of its immediate environment.
However, one must revert to the science of complexity to understand the long-term challenges of a winner-take-all mechanism. We have already seen the example that what is good for the individual bull-elk might not be the best for the species in the long-term. We see that super-linear scaling systems also emits significant negative by-products. Thus, the question that we need to ask is whether the organizations are paradoxically cultivating their own seeds of destruction in their ambitions of pursuing scale and market entrenchment.
Managing Scale
| I think the most difficult thing had been scaling the infrastructure. Trying to support the response we had received from our users and the number of people that were interested in using the software. – Shawn Fanning |
Froude’s number? It is defined as the square of the ship’s velocity divided by its length and multiplied by the acceleration caused by gravity. So why are we introducing ships in this chapter? As I have done before, I am liberally standing on the shoulder of the giant, Geoffrey West, and borrowing from his account on the importance of the Froude’s number and the practical implications. Since ships are subject to turbulence, using a small model that works in a simulated turbulent environment might not work when we manufacture a large ship that is facing the ebbs and troughs of a finicky ocean. The workings and impact of turbulence is very complex, and at scale it becomes even more complex. Froude’s key contribution was to figure out a mathematical pathway of how to efficiently and effectively scale from a small model to a practical object. He did that by using a ratio as the common denominator. Mr. West provides an example that hits home: How fast does a 10-foot-long ship have to move to mimic the motion of a 700-foot-long ship moving at 20 knots. If they are to have the same Froude number (that is, the same value of the square of their velocity divided by their length), then the velocity has to scale as the square root of their lengths. The ratio of the square root of their lengths is the the square of 700 feet of the ship/10 feet of the model ship which turns out to be the square of 70. For the 10-foot model to mimic the motion of a large ship, it must move at the speed of 20 knots/ square of 70 or 2.5 knots. The Froude number is still widely used across many fields today to bridge small scale and large-scale thinking. Although this number applies to physical systems, the notion that adaptive systems can be similarly bridged through appropriate mathematical equations. Unfortunately, because of the increased number of variables impacting adaptive systems and all of these variables working and learning from one another, the task of establishing a Froude number becomes diminishingly small.
The other concept that has gained wide attention is the science of allometry. Allometry essentially states that as size increases, then the form of the object would change. Allometric scaling governs all complex physical and adaptive systems. So the question is whether there are some universal laws or mathematics that can be used to enable us to better understand or predict scale impacts. Let us extend this thinking a bit further. If sizes influence form and form constitute all sub-physical elements, then it would stand to reason that a universal law or a set of equations can provide deep explanatory powers on scale and systems. One needs to bear in mind that even what one might consider a universal law might be true within finite observations and boundaries. In other words, if there are observations that fall outside of those boundaries, one is forced into resetting our belief in the universal law or to frame a new paradigm to cover these exigencies. I mention this because as we seek to understand business and global grand challenges considering the existence of complexity, scale, chaos and seeming disorder – we might also want to embrace multiple laws or formulations working at different hierarchies and different data sets to arrive at satisficing solutions to the problems that we want to wrestle with.
Physics and mathematics allow a qualitatively high degree of predictability. One can craft models across different scales to make a sensible approach on how to design for scale. If you were to design a prototype using a 3D printer and decide to scale that prototype a 100X, there are mathematical scalar components that are factored into the mechanics to allow for some sort of equivalence which would ultimately lead to the final product fulfilling its functional purpose in a complex physical system. But how does one manage scale in light of those complex adaptive systems that emerge due to human interactions, evolution of organization, uncertainty of the future, and dynamic rules that could rapidly impact the direction of a company?
Is scale a single measure? Or is it a continuum? In our activities, we intentionally or unintentionally invoke scale concepts. What is the most efficient scale to measure an outcome, so we can make good policy decisions, how do we apply our learning from one scale to a system that operates on another scale and how do we assess how sets of phenomena operate at different scales, spatially and temporally, and how they impact one another? Now the most interesting question: Is scale polymorphous? Does the word scale have different meanings in different contexts? When we talk about microbiology, we are operating at micro-scales. When we talk at a very macro level, our scales are huge. In business, we regard scale with respect to how efficiently we grow. In one way, it is a measure but for the following discussion, we will interpret scale as non-linear growth expending fewer and fewer resources to support that growth as a ratio.
As we had discussed previously, complex adaptive systems self-organize over time. They arrive at some steady state outcome without active intervention. In fact, the active intervention might lead to unintended consequences that might even spell doom for the system that is being influenced. So as an organization scales, it is important to keep this notion of rapid self-organization in mind which will inform us to make or not make certain decisions from a central or top-down perspective. In other words, part of managing scale successfully is to not manage it at a coarse-grained level.
The second element of successfully managing scale is to understand the constraints that prevent scale. There is an entire chapter dedicated to the theory of constraints which sheds light on why this is a fundamental process management technique that increases the pace of the system. But for our purposes in this section, we will summarize as follows: every system as it grows have constraints. It is important to understand the constraints because these constraints slow the system: the bottlenecks have to be removed. And once one constraint is removed, then one comes across another constraint. The system is a chain of events and it is imperative that all of these events are identified. The weakest links harangue the systems and these weakest links have to be either cleared or resourced to enable the system to scale. It is a continuous process of observation and tweaking the results with the established knowledge that the demons of uncertainty and variability can reset the entire process and one might have to start again. Despite that fact, constraint management is an effective method to negotiate and manage scale.
The third element is devising the appropriate organization architecture. As one projects into the future, management might be inclined toward developing and investing in the architecture early to accommodate the scale. Overinvestment in the architecture might not be efficient. As mentioned, cities and social systems that grow 100% require 85% investment in infrastructure: in other words, systems grow on a sublinear scale from an infrastructure perspective. How does management of scale arrive at the 85%? It is nigh impossible, but it is important to reserve that concept since it informs management to architect the infrastructure cautiously. Large investments upfront could be a waste or could slow the system down: alternative, investments that are postponed a little too late can also impact the system adversely.
The fourth element of managing scale is to focus your lens of opportunity. In macroecology, we can arrive at certain conclusions when we regard the system from a distance versus very closely. We can subsume our understanding into one big bucket called climate change and then we figure out different ways to manage the complexity that causes the climate change by invoking certain policies and incentives at a macro level. However, if we go closer, we might decide to target a very specific contributor to climate change – namely, fossil fuels. The theory follows that to manage the dynamic complexity and scale of climate impact – it would be best to address a major factor which, in this case, would be fossil fuels. The equivalence of this in a natural business setting would be to establish and focus the strategy for scale in a niche vertical or a relatively narrower set of opportunities. Even though we are working in the web of complex adaptive systems, we might devise strategies to directionally manage the business within the framework of complex physical systems where we have an understanding of the slight variations of initial state and the realization that the final outcome might be broad but yet bounded for intentional management.
The final element is the management of initial states. Complex physical systems are governed by variation in initial states. Perturbation of these initial states can lead to a wide divergence of outcomes, albeit bounded within a certain frame of reference. It is difficult perhaps to gauge all the interactions that might occur from a starting point to the outcome, although we agree that a few adjustments like decentralization of decision making, constraint management, optimal organization structure and narrowing the playing field would be helpful.
Internal versus External Scale
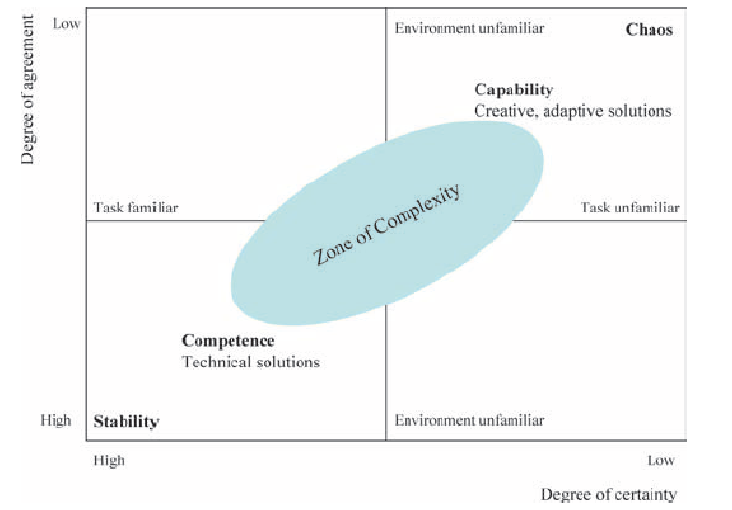
This article discusses internal and external complexity before we tee up a more detailed discussion on internal versus external scale. This chapter acknowledges that complex adaptive systems have inherent internal and external complexities which are not additive. The impact of these complexities is exponential. Hence, we have to sift through our understanding and perhaps even review the salient aspects of complexity science which have already been covered in relatively more detail in earlier chapter. However, revisiting complexity science is important, and we will often revisit this across other blog posts to really hit home the fundamental concepts and its practical implications as it relates to management and solving challenges at a business or even a grander social scale.
A complex system is a part of a larger environment. It is a safe to say that the larger environment is more complex than the system itself. But for the complex system to work, it needs to depend upon a certain level of predictability and regularity between the impact of initial state and the events associated with it or the interaction of the variables in the system itself. Note that I am covering both – complex physical systems and complex adaptive systems in this discussion. A system within an environment has an important attribute: it serves as a receptor to signals of external variables of the environment that impact the system. The system will either process that signal or discard the signal which is largely based on what the system is trying to achieve. We will dedicate an entire article on system engineering and thinking later, but the uber point is that a system exists to serve a definite purpose. All systems are dependent on resources and exhibits a certain capacity to process information. Hence, a system will try to extract as many regularities as possible to enable a predictable dynamic in an efficient manner to fulfill its higher-level purpose.
Let us understand external complexities. We can interchangeably use the word environmental complexity as well. External complexity represents physical, cultural, social, and technological elements that are intertwined. These environments beleaguered with its own grades of complexity acts as a mold to affect operating systems that are mere artifacts. If operating systems can fit well within the mold, then there is a measure of fitness or harmony that arises between an internal complexity and external complexity. This is the root of dynamic adaptation. When external environments are very complex, that means that there are a lot of variables at play and thus, an internal system has to process more information in order to survive. So how the internal system will react to external systems is important and they key bridge between those two systems is in learning. Does the system learn and improve outcomes on account of continuous learning and does it continually modify its existing form and functional objectives as it learns from external complexity? How is the feedback loop monitored and managed when one deals with internal and external complexities? The environment generates random problems and challenges and the internal system has to accept or discard these problems and then establish a process to distribute the problems among its agents to efficiently solve those problems that it hopes to solve for. There is always a mechanism at work which tries to align the internal complexity with external complexity since it is widely believed that the ability to efficiently align the systems is the key to maintaining a relatively competitive edge or intentionally making progress in solving a set of important challenges.
Internal complexity are sub-elements that interact and are constituents of a system that resides within the larger context of an external complex system or the environment. Internal complexity arises based on the number of variables in the system, the hierarchical complexity of the variables, the internal capabilities of information pass-through between the levels and the variables, and finally how it learns from the external environment. There are five dimensions of complexity: interdependence, diversity of system elements, unpredictability and ambiguity, the rate of dynamic mobility and adaptability, and the capability of the agents to process information and their individual channel capacities.
If we are discussing scale management, we need to ask a fundamental question. What is scale in the context of complex systems? Why do we manage for scale? How does management for scale advance us toward a meaningful outcome? How does scale compute in internal and external complex systems? What do we expect to see if we have managed for scale well? What does the future bode for us if we assume that we have optimized for scale and that is the key objective function that we have to pursue?
Model Thinking
| Model Framework |
The fundamental tenet of theory is the concept of “empiria“. Empiria refers to our observations. Based on observations, scientists and researchers posit a theory – it is part of scientific realism.
A scientific model is a causal explanation of how variables interact to produce a phenomenon, usually linearly organized. A model is a simplified map consisting of a few, primary variables that is gauged to have the most explanatory powers for the phenomenon being observed. We discussed Complex Physical Systems and Complex Adaptive Systems early on this chapter. It is relatively easier to map CPS to models than CAS, largely because models become very unwieldy as it starts to internalize more variables and if those variables have volumes of interaction between them. A simple analogy would be the use of multiple regression models: when you have a number of independent variables that interact strongly between each other, autocorrelation errors occur, and the model is not stable or does not have predictive value.
Research projects generally tend to either look at a case study or alternatively, they might describe a number of similar cases that are logically grouped together. Constructing a simple model that can be general and applied to many instances is difficult, if not impossible. Variables are subject to a researcher’s lack of understanding of the variable or the volatility of the variable. What further accentuates the problem is that the researcher misses on the interaction of how the variables play against one another and the resultant impact on the system. Thus, our understanding of our system can be done through some sort of model mechanics but, yet we share the common belief that the task of building out a model to provide all of the explanatory answers are difficult, if not impossible. Despite our understanding of our limitations of modeling, we still develop frameworks and artifact models because we sense in it a tool or set of indispensable tools to transmit the results of research to practical use cases. We boldly generalize our findings from empiria into general models that we hope will explain empiria best. And let us be mindful that it is possible – more so in the CAS systems than CPS that we might have multiple models that would fight over their explanatory powers simply because of the vagaries of uncertainty and stochastic variations.
Popper says: “Science does not rest upon rock-bottom. The bold structure of its theories rises, as it were, above a swamp. It is like a building erected on piles. The piles are driven down from above into the swamp, but not down to any natural or ‘given’ base; and when we cease our attempts to drive our piles into a deeper layer, it is not because we have reached firm ground. We simply stop when we are satisfied that they are firm enough to carry the structure, at least for the time being”. This leads to the satisficing solution: if a model can choose the least number of variables to explain the greatest amount of variations, the model is relatively better than other models that would select more variables to explain the same. In addition, there is always a cost-benefit analysis to be taken into consideration: if we add x number of variables to explain variation in the outcome but it is not meaningfully different than variables less than x, then one would want to fall back on the less-variable model because it is less costly to maintain.
Researchers must address three key elements in the model: time, variation and uncertainty. How do we craft a model which reflects the impact of time on the variables and the outcome? How to present variations in the model? Different variables might vary differently independent of one another. How do we present the deviation of the data in a parlance that allows us to make meaningful conclusions regarding the impact of the variations on the outcome? Finally, does the data that is being considered are actual or proxy data? Are the observations approximate? How do we thus draw the model to incorporate the fuzziness: would confidence intervals on the findings be good enough?
Two other equally other concepts in model design is important: Descriptive Modeling and Normative Modeling.
Descriptive models aim to explain the phenomenon. It is bounded by that goal and that goal only.
There are certain types of explanations that they fall back on: explain by looking at data from the past and attempting to draw a cause and effect relationship. If the researcher is able to draw a complete cause and effect relationship that meets the test of time and independent tests to replicate the results, then the causality turns into law for the limited use-case or the phenomenon being explained. Another explanation method is to draw upon context: explaining a phenomenon by looking at the function that the activity fulfills in its context. For example, a dog barks at a stranger to secure its territory and protect the home. The third and more interesting type of explanation is generally called intentional explanation: the variables work together to serve a specific purpose and the researcher determines that purpose and thus, reverse engineers the understanding of the phenomenon by understanding the purpose and how the variables conform to achieve that purpose.
This last element also leads us to thinking through the other method of modeling – namely, normative modeling. Normative modeling differs from descriptive modeling because the target is not to simply just gather facts to explain a phenomenon, but rather to figure out how to improve or change the phenomenon toward a desirable state. The challenge, as you might have already perceived, is that the subjective shadow looms high and long and the ultimate finding in what would be a normative model could essentially be a teleological representation or self-fulfilling prophecy of the researcher in action. While this is relatively more welcome in a descriptive world since subjectivism is diffused among a larger group that yields one solution, it is not the best in a normative world since variation of opinions that reflect biases can pose a problem.
How do we create a representative model of a phenomenon? First, we weigh if the phenomenon is to be understood as a mere explanation or to extend it to incorporate our normative spin on the phenomenon itself. It is often the case that we might have to craft different models and then weigh one against the other that best represents how the model can be explained. Some of the methods are fairly simple as in bringing diverse opinions to a table and then agreeing upon one specific model. The advantage of such an approach is that it provides a degree of objectivism in the model – at least in so far as it removes the divergent subjectivity that weaves into the various models. Other alternative is to do value analysis which is a mathematical method where the selection of the model is carried out in stages. You define the criteria of the selection and then the importance of the goal (if that be a normative model). Once all of the participants have a general agreement, then you have the makings of a model. The final method is to incorporate all all of the outliers and the data points in the phenomenon that the model seeks to explain and then offer a shared belief into those salient features in the model that would be best to apply to gain information of the phenomenon in a predictable manner.
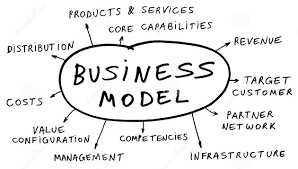
There are various languages that are used for modeling:
Written Language refers to the natural language description of the model. If price of butter goes up, the quantity demanded of the butter will go down. Written language models can be used effectively to inform all of the other types of models that follow below. It often goes by the name of “qualitative” research, although we find that a bit limiting. Just a simple statement like – This model approximately reflects the behavior of people living in a dense environment …” could qualify as a written language model that seeks to shed light on the object being studied.
Icon Models refer to a pictorial representation and probably the earliest form of model making. It seeks to only qualify those contours or shapes or colors that are most interesting and relevant to the object being studied. The idea of icon models is to pictorially abstract the main elements to provide a working understanding of the object being studied.
Topological Models refer to how the variables are placed with respect to one another and thus helps in creating a classification or taxonomy of the model. Once can have logical trees, class trees, Venn diagrams, and other imaginative pictorial representation of fields to further shed light on the object being studied. In fact, pictorial representations must abide by constant scale, direction and placements. In other words, if the variables are placed on a different scale on different maps, it would be hard to draw logical conclusions by sight alone. In addition, if the placements are at different axis in different maps or have different vectors, it is hard to make comparisons and arrive at a shared consensus and a logical end result.
Arithmetic Models are what we generally fall back on most. The data is measured with an arithmetic scale. It is done via tables, equations or flow diagrams. The nice thing about arithmetic models is that you can show multiple dimensions which is not possible with other modeling languages. Hence, the robustness and the general applicability of such models are huge and thus is widely used as a key language to modeling.
Analogous Models refer to crafting explanations using the power of analogy. For example, when we talk about waves – we could be talking of light waves, radio waves, historical waves, etc. These metaphoric representations can be used to explain phenomenon, but at best, the explanatory power is nebulous, and it would be difficult to explain the variations and uncertainties between two analogous models. However, it still is used to transmit information quickly through verbal expressions like – “Similarly”, “Equivalently”, “Looks like ..” etc. In fact, extrapolation is a widely used method in modeling and we would ascertain this as part of the analogous model to a great extent. That is because we time-box the variables in the analogous model to one instance and the extrapolated model to another instance and we tie them up with mathematical equations.
Linked Stars Blog 