Froude’s number? It is defined as the square of the ship’s velocity divided by its length and multiplied by the acceleration caused by gravity. So why are we introducing ships in this chapter? As I have done before, I am liberally standing on the shoulder of the giant, Geoffrey West, and borrowing from his account on the importance of the Froude’s number and the practical implications. Since ships are subject to turbulence, using a small model that works in a simulated turbulent environment might not work when we manufacture a large ship that is facing the ebbs and troughs of a finicky ocean. The workings and impact of turbulence is very complex, and at scale it becomes even more complex. Froude’s key contribution was to figure out a mathematical pathway of how to efficiently and effectively scale from a small model to a practical object. He did that by using a ratio as the common denominator. Mr. West provides an example that hits home: How fast does a 10-foot-long ship have to move to mimic the motion of a 700-foot-long ship moving at 20 knots. If they are to have the same Froude number (that is, the same value of the square of their velocity divided by their length), then the velocity has to scale as the square root of their lengths. The ratio of the square root of their lengths is the the square of 700 feet of the ship/10 feet of the model ship which turns out to be the square of 70.  For the 10-foot model to mimic the motion of a large ship, it must move at the speed of 20 knots/ square of 70 or 2.5 knots. The Froude number is still widely used across many fields today to bridge small scale and large-scale thinking. Although this number applies to physical systems, the notion that adaptive systems can be similarly bridged through appropriate mathematical equations. Unfortunately, because of the increased number of variables impacting adaptive systems and all of these variables working and learning from one another, the task of establishing a Froude number becomes diminishingly small.

The other concept that has gained wide attention is the science of allometry. Allometry essentially states that as size increases, then the form of the object would change. Allometric scaling governs all complex physical and adaptive systems. So the question is whether there are some universal laws or mathematics that can be used to enable us to better understand or predict scale impacts. Let us extend this thinking a bit further. If sizes influence form and form constitute all sub-physical elements, then it would stand to reason that a universal law or a set of equations can provide deep explanatory powers on scale and systems. One needs to bear in mind that even what one might consider a universal law might be true within finite observations and boundaries. In other words, if there are observations that fall outside of those boundaries, one is forced into resetting our belief in the universal law or to frame a new paradigm to cover these exigencies. I mention this because as we seek to understand business and global grand challenges considering the existence of complexity, scale, chaos and seeming disorder – we might also want to embrace multiple laws or formulations working at different hierarchies and different data sets to arrive at satisficing solutions to the problems that we want to wrestle with.

Physics and mathematics allow a qualitatively high degree of predictability. One can craft models across different scales to make a sensible approach on how to design for scale. If you were to design a prototype using a 3D printer and decide to scale that prototype a 100X, there are mathematical scalar components that are factored into the mechanics to allow for some sort of equivalence which would ultimately lead to the final product fulfilling its functional purpose in a complex physical system. But how does one manage scale in light of those complex adaptive systems that emerge due to human interactions, evolution of organization, uncertainty of the future, and dynamic rules that could rapidly impact the direction of a company?

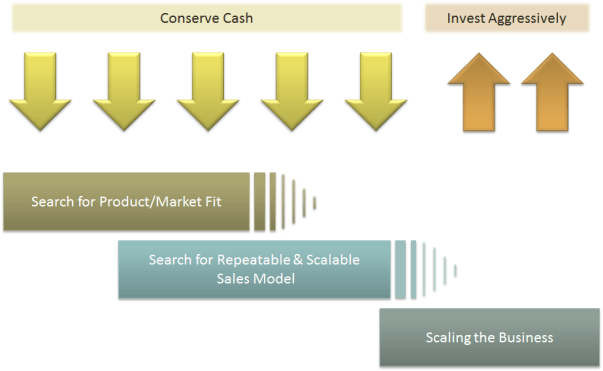
Is scale a single measure? Or is it a continuum? In our activities, we intentionally or unintentionally invoke scale concepts. What is the most efficient scale to measure an outcome, so we can make good policy decisions, how do we apply our learning from one scale to a system that operates on another scale and how do we assess how sets of phenomena operate at different scales, spatially and temporally, and how they impact one another? Now the most interesting question: Is scale polymorphous? Does the word scale have different meanings in different contexts? When we talk about microbiology, we are operating at micro-scales. When we talk at a very macro level, our scales are huge. In business, we regard scale with respect to how efficiently we grow. In one way, it is a measure but for the following discussion, we will interpret scale as non-linear growth expending fewer and fewer resources to support that growth as a ratio.

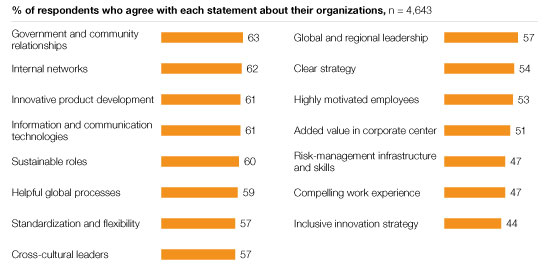
As we had discussed previously, complex adaptive systems self-organize over time. They arrive at some steady state outcome without active intervention. In fact, the active intervention might lead to unintended consequences that might even spell doom for the system that is being influenced. So as an organization scales, it is important to keep this notion of rapid self-organization in mind which will inform us to make or not make certain decisions from a central or top-down perspective. In other words, part of managing scale successfully is to not manage it at a coarse-grained level.

The second element of successfully managing scale is to understand the constraints that prevent scale. There is an entire chapter dedicated to the theory of constraints which sheds light on why this is a fundamental process management technique that increases the pace of the system. But for our purposes in this section, we will summarize as follows: every system as it grows have constraints. It is important to understand the constraints because these constraints slow the system: the bottlenecks have to be removed. And once one constraint is removed, then one comes across another constraint. The system is a chain of events and it is imperative that all of these events are identified. The weakest links harangue the systems and these weakest links have to be either cleared or resourced to enable the system to scale. It is a continuous process of observation and tweaking the results with the established knowledge that the demons of uncertainty and variability can reset the entire process and one might have to start again. Despite that fact, constraint management is an effective method to negotiate and manage scale.

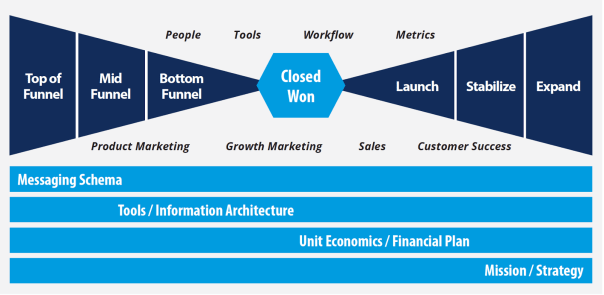
The third element is devising the appropriate organization architecture. As one projects into the future, management might be inclined toward developing and investing in the architecture early to accommodate the scale. Overinvestment in the architecture might not be efficient. As mentioned, cities and social systems that grow 100% require 85% investment in infrastructure: in other words, systems grow on a sublinear scale from an infrastructure perspective. How does management of scale arrive at the 85%? It is nigh impossible, but it is important to reserve that concept since it informs management to architect the infrastructure cautiously. Large investments upfront could be a waste or could slow the system down: alternative, investments that are postponed a little too late can also impact the system adversely.

The fourth element of managing scale is to focus your lens of opportunity. In macroecology, we can arrive at certain conclusions when we regard the system from a distance versus very closely. We can subsume our understanding into one big bucket called climate change and then we figure out different ways to manage the complexity that causes the climate change by invoking certain policies and incentives at a macro level. However, if we go closer, we might decide to target a very specific contributor to climate change – namely, fossil fuels. The theory follows that to manage the dynamic complexity and scale of climate impact – it would be best to address a major factor which, in this case, would be fossil fuels. The equivalence of this in a natural business setting would be to establish and focus the strategy for scale in a niche vertical or a relatively narrower set of opportunities. Even though we are working in the web of complex adaptive systems, we might devise strategies to directionally manage the business within the framework of complex physical systems where we have an understanding of the slight variations of initial state and the realization that the final outcome might be broad but yet bounded for intentional management.

The final element is the management of initial states. Complex physical systems are governed by variation in initial states. Perturbation of these initial states can lead to a wide divergence of outcomes, albeit bounded within a certain frame of reference. It is difficult perhaps to gauge all the interactions that might occur from a starting point to the outcome, although we agree that a few adjustments like decentralization of decision making, constraint management, optimal organization structure and narrowing the playing field would be helpful.