Category Archives: Chaos
The Finance Playbook for Scaling Complexity Without Chaos
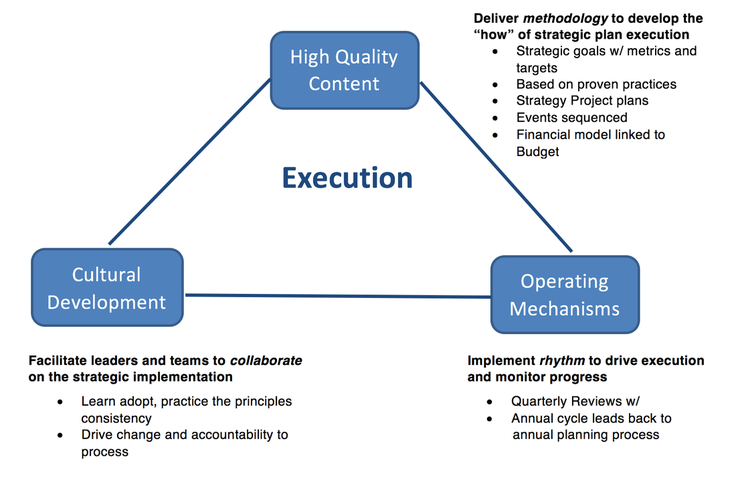
From Controlled Growth to Operational Grace
Somewhere between Series A optimism and Series D pressure sits the very real challenge of scale. Not just growth for its own sake but growth with control, precision, and purpose. A well-run finance function becomes less about keeping the lights on and more about lighting the runway. I have seen it repeatedly. You can double ARR, but if your deal desk, revenue operations, or quote-to-cash processes are even slightly out of step, you are scaling chaos, not a company.
Finance does not scale with spreadsheets and heroics. It scales with clarity. With every dollar, every headcount, and every workflow needing to be justified in terms of scale, simplicity must be the goal. I recall sitting in a boardroom where the CEO proudly announced a doubling of the top line. But it came at the cost of three overlapping CPQ systems, elongated sales cycles, rogue discounting, and a pipeline no one trusted. We did not have a scale problem. We had a complexity problem disguised as growth.
OKRs Are Not Just for Product Teams
When finance is integrated into company OKRs, magic happens. We begin aligning incentives across sales, legal, product, and customer success teams. Suddenly, the sales operations team is not just counting bookings but shaping them. Deal desk isn’t just a speed bump before legal review, but a value architect. Our quote-to-cash process is no longer a ticketing system but a flywheel for margin expansion.
At a Series B company, their shift began by tying financial metrics directly to the revenue team’s OKRs. Quota retirement was not enough. They measured the booked gross margin. Customer acquisition cost. Implementation of velocity. The sales team was initially skeptical but soon began asking more insightful questions. Deals that initially appeared promising were flagged early. Others that seemed too complicated were simplified before they even reached RevOps. Revenue is often seen as art. But finance gives it rhythm.
Scaling Complexity Despite the Chaos
The truth is that chaos is not the enemy of scale. Chaos is the cost of momentum. Every startup that is truly growing at a pace inevitably creates complexity. Systems become tangled. Roles blur. Approvals drift. That is not failure. That is physics. What separates successful companies is not the absence of chaos but their ability to organize it.
I often compare this to managing a growing city. You do not stop new buildings from going up just because traffic worsens. You introduce traffic lights, zoning laws, and transit systems that support the growth. In finance, that means being ready to evolve processes as soon as growth introduces friction. It means designing modular systems where complexity is absorbed rather than resisted. You do not simplify the growth. You streamline the experience of growing. Read Scale by Geoffrey West. Much of my interest in complexity theory and architecture for scale comes from it. Also, look out for my book, which will be published in February 2026: Complexity and Scale: Managing Order from Chaos. This book aligns literature in complexity theory with the microeconomics of scaling vectors and enterprise architecture.
At a late-stage Series C company, the sales motion had shifted from land-and-expand to enterprise deals with multi-year terms and custom payment structures. The CPQ tool was unable to keep up. Rather than immediately overhauling the tool, they developed middleware logic that routed high-complexity deals through a streamlined approval process, while allowing low-risk deals to proceed unimpeded. The system scaled without slowing. Complexity still existed, but it no longer dictated pace.
Cash Discipline: The Ultimate Growth KPI
Cash is not just oxygen. It is alignment. When finance speaks early and often about burn efficiency, marginal unit economics, and working capital velocity, we move from gatekeepers to enablers. I often remind founders that the cost of sales is not just the commission plan. It’s in the way deals are structured. It’s in how fast a contract can be approved. It’s in how many hands a quote needs to pass through.
At one Series A professional services firm, they introduced a “Deal ROI Calculator” at the deal desk. It calculated not just price and term but implementation effort, support burden, and payback period. The result was staggering. Win rates remained stable, but average deal profitability increased by 17 percent. Sales teams began choosing deals differently. Finance was not saying no. It was saying, “Say yes, but smarter.”
Velocity is a Decision, Not a Circumstance
The best-run companies are not faster because they have fewer meetings. They are faster because decisions are closer to the data. Finance’s job is to put insight into the hands of those making the call. The goal is not to make perfect decisions. It is to make the best decision possible with the available data and revisit it quickly.
In one post-Series A firm, we embedded finance analysts inside revenue operations. It blurred the traditional lines but sped up decision-making. Discount approvals have been reduced from 48 hours to 12-24 hours. Pricing strategies became iterative. A finance analyst co-piloted the forecast and flagged gaps weeks earlier than our CRM did. It wasn’t about more control. It was about more confidence.
When Process Feels Like Progress
It is tempting to think that structure slows things down. However, the right QTC design can unlock margin, trust, and speed simultaneously. Imagine a deal desk that empowers sales to configure deals within prudent guardrails. Or a contract management workflow that automatically flags legal risks. These are not dreams. These are the functions we have implemented.
The companies that scale well are not perfect. But their finance teams understand that complexity compounds quietly. And so, we design our systems not to prevent chaos but to make good decisions routine. We don’t wait for the fire drill. We design out the fire.
Make Your Revenue Operations Your Secret Weapon
If your finance team still views sales operations as a reporting function, you are underutilizing a strategic lever. Revenue operations, when empowered, can close the gap between bookings and billings. They can forecast with precision. They can flag incentive misalignment. One of the best RevOps leaders I worked with used to say, “I don’t run reports. I run clarity.” That clarity was worth more than any point solution we bought.
In scaling environments, automation is not optional. But automation alone does not save a broken process. Finance must own the blueprint. Every system, from CRM to CPQ to ERP, must speak the same language. Data fragmentation is not just annoying. It is value-destructive.
What Should You Do Now?
Ask yourself: Does finance have visibility into every step of the revenue funnel? Do our QTC processes support strategic flexibility? Is our deal desk a source of friction or a source of enablement? Can our sales comp plan be audited and justified in a board meeting without flinching?
These are not theoretical. They are the difference between Series C confusion and Series D confidence.
Let’s Make This Personal
I have seen incredible operators get buried under process debt because they mistook motion for progress. I have seen lean finance teams punch above their weight because they anchored their operating model in OKRs, cash efficiency, and rapid decision cycles. I have also seen the opposite. A sales ops function sitting in the corner. A deal desk no one trusts. A QTC process where no one knows who owns what.
These are fixable. But only if finance decides to lead. Not just report.
So here is my invitation. If you are a CFO, a CRO, a GC, or a CEO reading this, take one day this quarter to walk your revenue path from lead to cash. Sit with the people who feel the friction. Map the handoffs. And then ask, is this how we scale with control? Do you have the right processes in place? Do you have the technology to activate the process and minimize the friction?
The CFO as Chief Option Architect: Embracing Uncertainty
Part I: Embracing the Options Mindset
This first half explores the philosophical and practical foundation of real options thinking, scenario-based planning, and the CFO’s evolving role in navigating complexity. The voice is grounded in experience, built on systems thinking, and infused with a deep respect for the unpredictability of business life.
I learned early that finance, for all its formulas and rigor, rarely rewards control. In one of my earliest roles, I designed a seemingly watertight budget, complete with perfectly reconciled assumptions and cash flow projections. The spreadsheet sang. The market didn’t. A key customer delayed a renewal. A regulatory shift in a foreign jurisdiction quietly unraveled a tax credit. In just six weeks, our pristine model looked obsolete. I still remember staring at the same Excel sheet and realizing that the budget was not a map, but a photograph, already out of date. That moment shaped much of how I came to see my role as a CFO. Not as controller-in-chief, but as architect of adaptive choices.
The world has only become more uncertain since. Revenue operations now sit squarely in the storm path of volatility. Between shifting buying cycles, hybrid GTM models, and global macro noise, what used to be predictable has become probabilistic. Forecasting a quarter now feels less like plotting points on a trendline and more like tracing potential paths through fog. It is in this context that I began adopting and later, championing, the role of the CFO as “Chief Option Architect.” Because when prediction fails, design must take over.
This mindset draws deeply from systems thinking. In complex systems, what matters is not control, but structure. A system that adapts will outperform one that resists. And the best way to structure flexibility, I have found, is through the lens of real options. Borrowed from financial theory, real options describe the value of maintaining flexibility under uncertainty. Instead of forcing an all-in decision today, you make a series of smaller decisions, each one preserving the right, but not the obligation, to act in a future state. This concept, though rooted in asset pricing, holds powerful relevance for how we run companies.
When I began modeling capital deployment for new GTM motions, I stopped thinking in terms of “budget now, or not at all.” Instead, I started building scenario trees. Each branch represented a choice: deploy full headcount at launch or split into a two-phase pilot with a learning checkpoint. Invest in a new product SKU with full marketing spend, or wait for usage threshold signals to pass before escalation. These decision trees capture something that most budgets never do—the reality of the paths not taken, the contingencies we rarely discuss. And most importantly, they made us better at allocating not just capital, but attention. I am sharing my Bible on this topic, which was referred to me by Dr. Alexander Cassuto at Cal State Hayward in the Econometrics course. It was definitely more pleasant and easier to read than Jiang’s book on Econometrics.
This change in framing altered my approach to every part of revenue operations. Take, for instance, the deal desk. In traditional settings, deal desk is a compliance checkpoint where pricing, terms, and margin constraints are reviewed. But when viewed through an options lens, the deal desk becomes a staging ground for strategic bets. A deeply discounted deal might seem reckless on paper, but if structured with expansion clauses, usage gates, or future upsell options, it can behave like a call option on account growth. The key is to recognize and price the option value. Once I began modeling deals this way, I found we were saying “yes” more often, and with far better clarity on risk.
Data analytics became essential here not for forecasting the exact outcome, but for simulating plausible ones. I leaned heavily on regression modeling, time-series decomposition, and agent-based simulation. We used R to create time-based churn scenarios across customer cohorts. We used Arena to simulate resource allocation under delayed expansion assumptions. These were not predictions. They were controlled chaos exercises, designed to show what could happen, not what would. But the power of this was not just in the results, but it was in the mindset it built. We stopped asking, “What will happen?” and started asking, “What could we do if it does?”
From these simulations, we developed internal thresholds to trigger further investment. For example, if three out of five expansion triggers were fired, such as usage spike, NPS improvement, and additional department adoption, then we would greenlight phase two of GTM spend. That logic replaced endless debate with a predefined structure. It also gave our board more confidence. Rather than asking them to bless a single future, we offered a roadmap of choices, each with its own decision gates. They didn’t need to believe our base case. They only needed to believe we had options.
Yet, as elegant as these models were, the most difficult challenge remained human. People, understandably, want certainty. They want confidence in forecasts, commitment to plans, and clarity in messaging. I had to coach my team and myself to get comfortable with the discomfort of ambiguity. I invoked the concept of bounded rationality from decision science: we make the best decisions we can with the information available to us, within the time allotted. There is no perfect foresight. There is only better framing.
This is where the law of unintended consequences makes its entrance. In traditional finance functions, overplanning often leads to rigidity. You commit to hiring plans that no longer make sense three months in. You promise CAC thresholds that collapse under macro pressure. You bake linearity into a market that moves in waves. When this happens, companies double down, pushing harder against the wrong wall. But when you think in options, you pull back when the signal tells you to. You course-correct. You adapt. And paradoxically, you appear more stable.
As we embedded this thinking deeper into our revenue operations, we also became more cross-functional. Sales began to understand the value of deferring certain go-to-market investments until usage signals validated demand. Product began to view feature development as portfolio choices: some high-risk, high-return, others safer but with less upside. Customer Success began surfacing renewal and expansion probabilities not as binary yes/no forecasts, but as weighted signals on a decision curve. The shared vocabulary of real options gave us a language for navigating ambiguity together.
We also brought this into our capital allocation rhythm. Instead of annual budget cycles, we moved to rolling forecasts with embedded thresholds. If churn stayed below 8% and expansion held steady, we would greenlight an additional five SDRs. If product-led growth signals in EMEA hit critical mass, we’d fund a localized support pod. These weren’t whims. They were contingent commitments, bound by logic, not inertia. And that changed everything.
The results were not perfect. We made wrong bets. Some options expired worthless. Others took longer to mature than we expected. But overall, we made faster decisions with greater alignment. We used our capital more efficiently. And most of all, we built a culture that didn’t flinch at uncertainty—but designed for it.
In the next part of this essay, I will go deeper into the mechanics of implementing this philosophy across the deal desk, QTC architecture, and pipeline forecasting. I will also show how to build dashboards that visualize decision trees and option paths, and how to teach your teams to reason probabilistically without losing speed. Because in a world where volatility is the only certainty, the CFO’s most enduring edge is not control, but it is optionality, structured by design and deployed with discipline.
Part II: Implementing Option Architecture Inside RevOps
A CFO cannot simply preach agility from a whiteboard. To embed optionality into the operational fabric of a company, the theory must show up in tools, in dashboards, in planning cadences, and in the daily decisions made by deal desks, revenue teams, and systems owners. I have found that fundamental transformation comes not from frameworks, but from friction—the friction of trying to make the idea work across functions, under pressure, and at scale. That’s where option thinking proves its worth.
We began by reimagining the deal desk, not as a compliance stop but as a structured betting table. In conventional models, deal desks enforce pricing integrity, review payment terms, and ensure T’s and C’s fall within approved tolerances. That’s necessary, but not sufficient. In uncertain environments—where customer buying behavior, competitive pressure, or adoption curves wobble without warning: rigid deal policies become brittle. The opportunity lies in recasting the deal desk as a decision node within a larger options tree.
Consider a SaaS enterprise deal involving land-and-expand potential. A rigid model forces either full commitment upfront or defers expansion, hoping for a vague “later.” But if we treat the deal like a compound call option, we see more apparent logic. You price the initial land deal aggressively, with usage-based triggers that, when met, unlock favorable expansion terms. You embed a re-pricing clause if usage crosses a defined threshold in 90 days. You insert a “soft commit” expansion clause tied to the active user count. None of these is just a term. They are embedded with real options. And when structured well, they deliver upside without requiring the customer to commit to uncertain future needs.
In practice, this approach meant reworking CPQ systems, retraining legal, and coaching reps to frame options credibly. We designed templates with optionality clauses already coded into Salesforce workflows. Once an account crossed a pre-defined trigger say, 80% license utilization, then the next best action flowed to the account executive and customer success manager. The logic wasn’t linear. It was branching. We visualized deal paths in a way that corresponds to mapping a decision tree in a risk-adjusted capital model.
Yet even the most elegant structure can fail if the operating rhythm stays linear. That is why we transitioned away from rigid quarterly forecasts toward rolling scenario-based planning. Forecasting ceased to be a spreadsheet contest. Instead, we evaluated forecast bands, not point estimates. If base churn exceeded X% in a specific cohort, how did that impact our expansion coverage ratio? If deal velocity in EMEA slowed by two weeks, how would that compress the bookings-to-billings gap? We visualized these as cascading outcomes, not just isolated misses.
To build this capability, we used what I came to call “option dashboards.” These were layered, interactive models with inputs tied to a live pipeline and post-sale telemetry. Each card on the dashboard represented a decision node—an inflection point. Would we deploy more headcount into SMB if the average CAC-to-LTV fell below 3:1? Would we pause feature rollout in one region to redirect support toward a segment with stronger usage signals? Each choice was pre-wired with boundary logic. The decisions didn’t live in a drawer—they lived in motion.
Building these dashboards required investment. But more than tools, it required permission. Teams needed to know they could act on signal, not wait for executive validation every time a deviation emerged. We institutionalized the language of “early signal actionability.” If revenue leaders spotted a decline in renewal health across a cluster of customers tied to the same integration module, they didn’t wait for a churn event. They pulled forward roadmap fixes. That wasn’t just good customer service, but it was real options in flight.
This also brought a new flavor to our capital allocation rhythm. Rather than annual planning cycles that locked resources into static swim lanes, we adopted gated resourcing tied to defined thresholds. Our FP&A team built simulation models in Python and R, forecasting the expected value of a resourcing move based on scenario weightings. For example, if a new vertical showed a 60% likelihood of crossing a 10-deal threshold by mid-Q3, we pre-approved GTM spend to activate contingent on hitting that signal. This looked cautious to some. But in reality, it was aggressive and in the right direction, at the right moment.
Throughout all of this, I kept returning to a central truth: uncertainty punishes rigidity, but rewards those who respect its contours. A pricing policy that cannot flex will leave margin on the table or kill deals in flight. A hiring plan that commits too early will choke working capital. And a CFO who waits for clarity before making bets will find they arrive too late. In decision theory, we often talk about “the cost of delay” versus “the cost of error.” A good options model minimizes both, which, interestingly, is not by being just right, but by being ready.
Of course, optionality without discipline can devolve into indecision. We embedded guardrails. We defined thresholds that made decision inertia unacceptable. If a cohort’s NRR dropped for three consecutive months and win-back campaigns failed, we sunsetted that motion. If a beta feature was unable to hit usage velocity within a quarter, we reallocated the development budget. These were not emotional decisions, but they were logical conclusions of failed options. And we celebrated them. A failed option, tested and closed, beats a zombie investment every time.
We also revised our communication with the board. Instead of defending fixed forecasts, we presented probability-weighted trees. “If churn holds, and expansion triggers fire, we’ll beat target by X.” “If macro shifts pull SMB renewals down by 5%, we stay within plan by flexing mid-market initiatives.” This shifted the conversation from finger-pointing to scenario readiness. Investors liked it. More importantly, so did the executive team. We could disagree on base assumptions but still align on decisions because we’d mapped the branches ahead of time.
One area where this thought made an outsized impact was compensation planning. Sales comp is notoriously fragile under volatility. We redesigned quota targets and commission accelerators using scenario bands, not fixed assumptions. We tested payout curves under best, base, and downside cases. We then ran Monte Carlo simulations to see how frequently actuals would fall into the “too much upside” or “demotivating downside” zones. This led to more durable comp plans, which meant fewer panicked mid-year resets. Our reps trusted the system. And our CFO team could model cost predictability with far greater confidence.
In retrospection, all these loops back to a single mindset shift: you don’t plan to be right. You plan to stay in the game. And staying in the game requires options that are well-designed, embedded into the process, and respected by every function. Sales needs to know they can escalate an expansion offer once particular customer signals fire. Success needs to know they have the budget authority to engage support when early churn flags arise. Product needs to know they can pause a roadmap stream if NPV no longer justifies it. And finance needs to know that its most significant power is not in control, but in preparation.
Today, when I walk into a revenue operations review or a strategic planning offsite, I do not bring a budget with fixed forecasts. I get a map. It has branches. It has signals. It has gates. And it has options, and each one designed not to predict the future, but to help us meet it with composure, and to move quickly when the fog clears.
Because in the world I have operated in, spanning economic cycles, geopolitical events, sudden buyer hesitation, system failures, and moments of exponential product success since 1994 until now, one principle has held. The companies that win are not the ones who guess right. They are the ones who remain ready. And readiness, I have learned, is the true hallmark of a great CFO.
AI and the Evolving Role of CFOs
For much of the twentieth century, the role of the Chief Financial Officer was understood in familiar terms. A steward of control. A master of precision. A guardian of the balance sheet. The CFO was expected to be meticulous, cautious, and above all, accountable. Decisions were made through careful deliberation. Assumptions were scrutinized. Numbers did not lie; they merely required interpretation. There was an art to the conservatism and a quiet pride in it. Order, after all, was the currency of good finance.
Then artificial intelligence arrived—not like a polite guest knocking at the door, but more like a storm bursting through the windows, unsettling assumptions, and rewriting the rules of what it means to manage the financial function. Suddenly, the world of structured inputs and predictable outputs became a dynamic theater of probabilities, models, and machine learning loops. The close of the quarter, once a ritual of discipline and human labor, was now something that could be shortened by algorithms. Forecasts, previously the result of sleepless nights and spreadsheets, could now be generated in minutes. And yet, beneath the glow of progress, a quieter question lingered in the minds of financial leaders: Are we still in control?
The paradox is sharp. AI promises greater accuracy, faster insights, and efficiencies that were once unimaginable. But it also introduces new vulnerabilities. Decisions made by machines cannot always be explained by humans. Data patterns shift, and models evolve in ways that are hard to monitor, let alone govern. The very automation that liberates teams from tedious work may also obscure how decisions are being made. For CFOs, whose role rests on the fulcrum of control and transparency, this presents a challenge unlike any other.
To understand what is at stake, one must first appreciate the philosophical shift taking place. Traditional finance systems were built around rules. If a transaction did not match a predefined criterion, it was flagged. If a value exceeded a threshold, it triggered an alert. There was a hierarchy to control. Approvals, audits, reconciliations—all followed a chain of accountability. AI, however, does not follow rules in the conventional sense. It learns patterns. It makes predictions. It adjusts based on what it sees. In place of linear logic, it offers probability. In place of rules, it gives suggestions.
This does not make AI untrustworthy, but it does make it unfamiliar. And unfamiliarity breeds caution. For CFOs who have spent decades refining control environments, AI is not merely a tool. It is a new philosophy of decision-making. And it is one that challenges the muscle memory of the profession.
What, then, does it mean to stay in control in an AI-enhanced finance function? It begins with visibility. CFOs must ensure that the models driving key decisions—forecasts, risk assessments, working capital allocations—are not black boxes. Every algorithm must come with a passport. What data went into it? What assumptions were made? How does it behave when conditions change? These are not technical questions alone. They are governance questions. And they sit at the heart of responsible financial leadership.
Equally critical is the quality of data. An AI model is only as reliable as the information it consumes. Dirty data, incomplete records, or inconsistent definitions can quickly derail the most sophisticated tools. In this environment, the finance function must evolve from being a consumer of data to a custodian of it. The general ledger, once a passive repository of transactions, becomes part of a living data ecosystem. Consistency matters. Lineage matters. And above all, context matters. A forecast that looks brilliant in isolation may collapse under scrutiny if it was trained on flawed assumptions.
But visibility and data are only the beginning. As AI takes on more tasks that were once performed by humans, the traditional architecture of control must be reimagined. Consider the principle of segregation of duties. In the old world, one person entered the invoice, another approved it, and a third reviewed the ledger. These checks and balances were designed to prevent fraud, errors, and concentration of power. But what happens when an AI model is performing all three functions? Who oversees the algorithm? Who reviews the reviewer?
The answer is not to retreat from automation, but to introduce new forms of oversight. CFOs must create protocols for algorithmic accountability. This means establishing thresholds for machine-generated recommendations, building escalation paths for exceptions, and defining moments when human judgement must intervene. It is not about mistrusting the machine. It is about ensuring that the machine is governed with the same discipline once reserved for people.
And then there is the question of resilience. AI introduces new dependencies—on data pipelines, on cloud infrastructures, on model stability. A glitch in a forecasting model could ripple through the entire enterprise plan. A misfire in an expense classifier could disrupt a close. These are not hypothetical risks. They are operational realities. Just as organizations have disaster recovery plans for cyber breaches or system outages, they must now develop contingency plans for AI failures. The models must be monitored. The outputs must be tested. And the humans must be prepared to take over when the automation stumbles.
Beneath all of this, however, lies a deeper cultural transformation. The finance team of the future will not be composed solely of accountants, auditors, and analysts. It will also include data scientists, machine learning specialists, and process architects. The rhythm of work will shift—from data entry and manual reconciliations to interpretation, supervision, and strategic advising. This demands a new kind of fluency. Not necessarily the ability to write code, but the ability to understand how AI works, what it can do, and where its boundaries lie.
This is not a small ask. It requires training, cross-functional collaboration, and a willingness to challenge tradition. But it also opens the door to a more intellectually rich finance function—one where humans and machines collaborate to generate insights that neither could have achieved alone.
If there is a guiding principle in all of this, it is that control does not mean resisting change. It means shaping it. For CFOs, the task is not to retreat into spreadsheets or resist the encroachment of algorithms. It is to lead the integration of intelligence into every corner of the finance operation. To set the standards, define the guardrails, and ensure that the organization embraces automation not as a surrender of responsibility, but as an evolution of it.
Because in the end, the goal is not simply to automate. It is to augment. Not to replace judgement, but to elevate it. Not to remove the human hand from finance, but to position it where it matters most: at the helm, guiding the ship through faster currents, with clearer vision and steadier hands.
Artificial intelligence may never match the emotional weight of human intuition. It may not understand the stakes behind a quarter’s earnings or the subtle implications of a line item in a note to shareholders. But it can free up time. It can provide clarity. It can make the financial function faster, more adaptive, and more resilient.
And if the CFO of the past was a gatekeeper, the CFO of the future will be a choreographer—balancing risk and intelligence, control and creativity, all while ensuring that the numbers, no matter how complex their origin, still tell a story that is grounded in truth.
The machines are here. They are learning. And they are listening. The challenge is not to contain them, but to guide them—thoughtfully, carefully, and with the discipline that has always defined great finance.
Because in this new world, control is not lost. It is simply redefined.
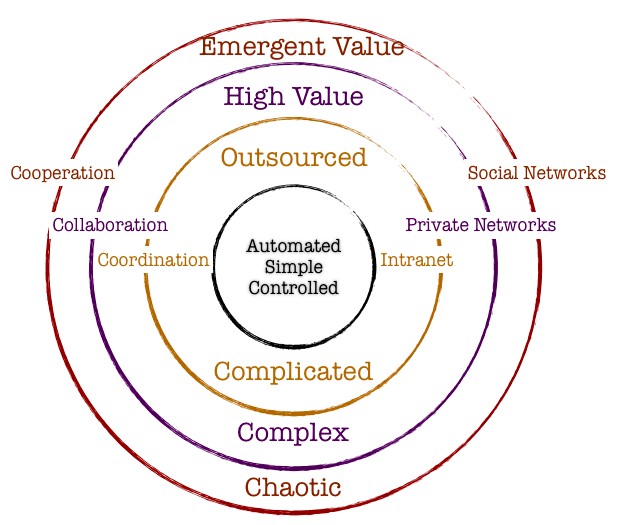
Navigating Chaos and Model Thinking
An inherent property of a chaotic system is that slight changes in initial conditions in the system result in a disproportionate change in outcome that is difficult to predict. Chaotic systems appear to create outcomes that appear to be random: they are generated by simple and non-random processes but the complexity of such systems emerge over time driven by numerous iterations of simple rules. The elements that compose chaotic systems might be few in number, but these elements work together to produce an intricate set of dynamics that amplifies the outcome and makes it hard to be predictable. These systems evolve over time, doing so according to rules and initial conditions and how the constituent elements work together.
Complex systems are characterized by emergence. The interactions between the elements of the system with its environment create new properties which influence the structural development of the system and the roles of the agents. In such systems there is self-organization characteristics that occur, and hence it is difficult to study and effect a system by studying the constituent parts that comprise it. The task becomes even more formidable when one faces the prevalent reality that most systems exhibit non-linear dynamics.
So how do we incorporate management practices in the face of chaos and complexity that is inherent in organization structure and market dynamics? It would be interesting to study this in light of the evolution of management principles in keeping with the evolution of scientific paradigms.
Newtonian Mechanics and Taylorism
Traditional organization management has been heavily influenced by Newtonian mechanics. The five key assumptions of Newtonian mechanics are:
- Reality is objective
- Systems are linear and there is a presumption that all underlying cause and effect are linear
- Knowledge is empirical and acquired through collecting and analyzing data with the focus on surfacing regularities, predictability and control
- Systems are inherently efficient. Systems almost always follows the path of least resistance
- If inputs and process is managed, the outcomes are predictable
Frederick Taylor is the father of operational research and his methods were deployed in automotive companies in the 1940’s. Workers and processes are input elements to ensure that the machine functions per expectations. There was a linearity employed in principle. Management role was that of observation and control and the system would best function under hierarchical operating principles. Mass and efficient production were the hallmarks of management goal.
Randomness and the Toyota Way
The randomness paradigm recognized uncertainty as a pervasive constant. The various methods that Toyota Way invoked around 5W rested on the assumption that understanding the cause and effect is instrumental and this inclined management toward a more process-based deployment. Learning is introduced in this model as a dynamic variable and there is a lot of emphasis on the agents and providing them the clarity and purpose of their tasks. Efficiencies and quality are presumably driven by the rank and file and autonomous decisions are allowed. The management principle moves away from hierarchical and top-down to a more responsibility driven labor force.
Complexity and Chaos and the Nimble Organization
Increasing complexity has led to more demands on the organization. With the advent of social media and rapid information distribution and a general rise in consciousness around social impact, organizations have to balance out multiple objectives. Any small change in initial condition can lead to major outcomes: an advertising mistake can become a global PR nightmare; a word taken out of context could have huge ramifications that might immediately reflect on the stock price; an employee complaint could force management change. Increasing data and knowledge are not sufficient to ensure long-term success. In fact, there is no clear recipe to guarantee success in an age fraught with non-linearity, emergence and disequilibrium. To succeed in this environment entails the development of a learning organization that is not governed by fixed top-down rules: rather the rules are simple and the guidance is around the purpose of the system or the organization. It is best left to intellectual capital to self-organize rapidly in response to external information to adapt and make changes to ensure organization resilience and success.
Companies are dynamic non-linear adaptive systems. The elements in the system are constantly interacting between themselves and their external environment. This creates new emergent properties that are sensitive to the initial conditions. A change in purpose or strategic positioning could set a domino effect and can lead to outcomes that are not predictable. Decisions are pushed out to all levels in the organization, since the presumption is that local and diverse knowledge that spontaneously emerge in response to stimuli is a superior structure than managing for complexity in a centralized manner. Thus, methods that can generate ideas, create innovation habitats, and embrace failures as providing new opportunities to learn are best practices that companies must follow. Traditional long-term planning and forecasting is becoming a far harder exercise and practically impossible. Thus, planning is more around strategic mindset, scenario planning, allowing local rules to auto generate without direct supervision, encourage dissent and diversity, stimulate creativity and establishing clarity of purpose and broad guidelines are the hall marks of success.
Principles of Leadership in a New Age
We have already explored the fact that traditional leadership models originated in the context of mass production and efficiencies. These models are arcane in our information era today, where systems are characterized by exponential dynamism of variables, increased density of interactions, increased globalization and interconnectedness, massive information distribution at increasing rapidity, and a general toward economies driven by free will of the participants rather than a central authority.
Complexity Leadership Theory (Uhl-Bien) is a “framework for leadership that enables the learning, creative and adaptive capacity of complex adaptive systems in knowledge-producing organizations or organizational units. Since planning for the long-term is virtually impossible, Leadership has to be armed with different tool sets to steer the organization toward achieving its purpose. Leaders take on enabler role rather than controller role: empowerment supplants control. Leadership is not about focus on traits of a single leader: rather, it redirects emphasis from individual leaders to leadership as an organizational phenomenon. Leadership is a trait rather than an individual. We recognize that complex systems have lot of interacting agents – in business parlance, which might constitute labor and capital. Introducing complexity leadership is to empower all of the agents with the ability to lead their sub-units toward a common shared purpose. Different agents can become leaders in different roles as their tasks or roles morph rapidly: it is not necessarily defined by a formal appointment or knighthood in title.
Thus, complexity of our modern-day reality demands a new strategic toolset for the new leader. The most important skills would be complex seeing, complex thinking, complex knowing, complex acting, complex trusting and complex being. (Elena Osmodo, 2012)
Complex Seeing: Reality is inherently subjective. It is a page of the Heisenberg Uncertainty principle that posits that the independence between the observer and the observed is not real. If leaders are not aware of this independence, they run the risk of engaging in decisions that are fraught with bias. They will continue to perceive reality with the same lens that they have perceived reality in the past, despite the fact that undercurrents and riptides of increasingly exponential systems are tearing away their “perceived reality.” Leader have to be conscious about the tectonic shifts, reevaluate their own intentions, probe and exclude biases that could cloud the fidelity of their decisions, and engage in a continuous learning process. The ability to sift and see through this complexity sets the initial condition upon which the entire system’s efficacy and trajectory rests.
Complex Thinking: Leaders have to be cognizant of falling prey to linear simple cause and effect thinking. On the contrary, leaders have to engage in counter-intuitive thinking, brainstorming and creative thinking. In addition, encouraging dissent, debates and diversity encourage new strains of thought and ideas.
Complex Feeling: Leaders must maintain high levels of energy and be optimistic of the future. Failures are not scoffed at; rather they are simply another window for learning. Leaders have to promote positive and productive emotional interactions. The leaders are tasked to increase positive feedback loops while reducing negative feedback mechanisms to the extent possible. Entropy and attrition taxes any system as is: the leader’s job is to set up safe environment to inculcate respect through general guidelines and leading by example.
Complex Knowing: Leadership is tasked with formulating simple rules to enable learned and quicker decision making across the organization. Leaders must provide a common purpose, interconnect people with symbols and metaphors, and continually reiterate the raison d’etre of the organization. Knowing is articulating: leadership has to articulate and be humble to any new and novel challenges and counterfactuals that might arise. The leader has to establish systems of knowledge: collective learning, collaborative learning and organizational learning. Collective learning is the ability of the collective to learn from experiences drawn from the vast set of individual actors operating in the system. Collaborative learning results due to interaction of agents and clusters in the organization. Learning organization, as Senge defines it, is “where people continually expand their capacity to create the results they truly desire, where new and expansive patterns of thinking are nurtured, where collective aspirations are set free, and where people are continually learning to see the whole together.”
Complex Acting: Complex action is the ability of the leader to not only work toward benefiting the agents in his/her purview, but also to ensure that the benefits resonates to a whole which by definition is greater than the sum of the parts. Complex acting is to take specific action-oriented steps that largely reflect the values that the organization represents in its environmental context.
Complex Trusting: Decentralization requires conferring power to local agents. For decentralization to work effectively, leaders have to trust that the agents will, in the aggregate, work toward advancing the organization. The cost of managing top-down is far more than the benefits that a trust-based decentralized system would work in a dynamic environment resplendent with the novelty of chaos and complexity.
Complex Being: This is the ability of the leaser to favor and encourage communication across the organization rapidly. The leader needs to encourage relationships and inter-functional dialogue.
The role of complex leaders is to design adaptive systems that are able to cope with challenging and novel environments by establishing a few rules and encouraging agents to self-organize autonomously at local levels to solve challenges. The leader’s main role in this exercise is to set the strategic directions and the guidelines and let the organizations run.
Chaos and the tide of Entropy!
We have discussed chaos. It is rooted in the fundamental idea that small changes in the initial condition in a system can amplify the impact on the final outcome in the system. Let us now look at another sibling in systems literature – namely, the concept of entropy. We will then attempt to bridge these two concepts since they are inherent in all systems.
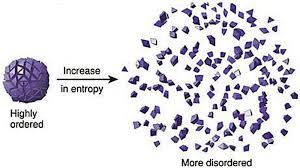
Entropy arises from the law of thermodynamics. Let us state all three laws:
- First law is known as the Lay of Conservation of Energy which states that energy can neither be created nor destroyed: energy can only be transferred from one form to another. Thus, if there is work in terms of energy transformation in a system, there is equivalent loss of energy transformation around the system. This fact balances the first law of thermodynamics.
- Second law of thermodynamics states that the entropy of any isolated system always increases. Entropy always increases, and rarely ever decreases. If a locker room is not tidied, entropy dictates that it will become messier and more disorderly over time. In other words, all systems that are stagnant will inviolably run against entropy which would lead to its undoing over time. Over time the state of disorganization increases. While energy cannot be created or destroyed, as per the First Law, it certainly can change from useful energy to less useful energy.
- Third law establishes that the entropy of a system approaches a constant value as the temperature approaches absolute zero. Thus, the entropy of a pure crystalline substance at absolute zero temperature is zero. However, if there is any imperfection that resides in the crystalline structure, there will be some entropy that will act upon it.
Entropy refers to a measure of disorganization. Thus people in a crowd that is widely spread out across a large stadium has high entropy whereas it would constitute low entropy if people are all huddled in one corner of the stadium. Entropy is the quantitative measure of the process – namely, how much energy has been spent from being localized to being diffused in a system. Entropy is enabled by motion or interaction of elements in a system, but is actualized by the process of interaction. All particles work toward spontaneously dissipating their energy if they are not curtailed from doing so. In other words, there is an inherent will, philosophically speaking, of a system to dissipate energy and that process of dissipation is entropy. However, it makes no effort to figure out how quickly entropy kicks into gear – it is this fact that makes it difficult to predict the overall state of the system.
Chaos, as we have already discussed, makes systems unpredictable because of perturbations in the initial state. Entropy is the dissipation of energy in the system, but there is no standard way of knowing the parameter of how quickly entropy would set in. There are thus two very interesting elements in systems that almost work simultaneously to ensure that predictability of systems become harder.
Another way of looking at entropy is to view this as a tax that the system charges us when it goes to work on our behalf. If we are purposefully calibrating a system to meet a certain purpose, there is inevitably a corresponding usage of energy or dissipation of energy otherwise known as entropy that is working in parallel. A common example that we are familiar with is mass industrialization initiatives. Mass industrialization has impacts on environment, disease, resource depletion, and a general decay of life in some form. If entropy as we understand it is an irreversible phenomenon, then there is virtually nothing that can be done to eliminate it. It is a permanent tax of varying magnitude in the system.
Humans have since early times have tried to formulate a working framework of the world around them. To do that, they have crafted various models and drawn upon different analogies to lend credence to one way of thinking over another. Either way, they have been left best to wrestle with approximations: approximations associated with their understanding of the initial conditions, approximations on model mechanics, approximations on the tax that the system inevitably charges, and the approximate distribution of potential outcomes. Despite valiant efforts to reduce the framework to physical versus behavioral phenomena, their final task of creating or developing a predictable system has not worked. While physical laws of nature describe physical phenomena, the behavioral laws describe non-deterministic phenomena. If linear equations are used as tools to understand the physical laws following the principles of classical Newtonian mechanics, the non-linear observations marred any consistent and comprehensive framework for clear understanding. Entropy reaches out toward an irreversible thermal death: there is an inherent fatalism associated with the Second Law of Thermodynamics. However, if that is presumed to be the case, how is it that human evolution has jumped across multiple chasms and have evolved to what it is today? If indeed entropy is the tax, one could argue that chaos with its bounded but amplified mechanics have allowed the human race to continue.
Let us now deliberate on this observation of Richard Feynmann, a Nobel Laurate in physics – “So we now have to talk about what we mean by disorder and what we mean by order. … Suppose we divide the space into little volume elements. If we have black and white molecules, how many ways could we distribute them among the volume elements so that white is on one side and black is on the other? On the other hand, how many ways could we distribute them with no restriction on which goes where? Clearly, there are many more ways to arrange them in the latter case.
We measure “disorder” by the number of ways that the insides can be arranged, so that from the outside it looks the same. The logarithm of that number of ways is the entropy. The number of ways in the separated case is less, so the entropy is less, or the “disorder” is less.” It is commonly also alluded to as the distinction between microstates and macrostates. Essentially, it says that there could be innumerable microstates although from an outsider looking in – there is only one microstate. The number of microstates hints at the system having more entropy.
In a different way, we ran across this wonderful example: A professor distributes chocolates to students in the class. He has 35 students but he distributes 25 chocolates. He throws those chocolates to the students and some students might have more than others. The students do not know that the professor had only 25 chocolates: they have presumed that there were 35 chocolates. So the end result is that the students are disconcerted because they perceive that the other students have more chocolates than they have distributed but the system as a whole shows that there are only 25 chocolates. Regardless of all of the ways that the 25 chocolates are configured among the students, the microstate is stable.
So what is Feynmann and the chocolate example suggesting for our purpose of understanding the impact of entropy on systems: Our understanding is that the reconfiguration or the potential permutations of elements in the system that reflect the various microstates hint at higher entropy but in reality has no impact on the microstate per se except that the microstate has inherently higher entropy. Does this mean that the macrostate thus has a shorter life-span? Does this mean that the microstate is inherently more unstable? Could this mean an exponential decay factor in that state? The answer to all of the above questions is not always. Entropy is a physical phenomenon but to abstract this out to enable a study of organic systems that represent super complex macrostates and arrive at some predictable pattern of decay is a bridge too far! If we were to strictly follow the precepts of the Second Law and just for a moment forget about Chaos, one could surmise that evolution is not a measure of progress, it is simply a reconfiguration.
Theodosius Dobzhansky, a well known physicist, says: “Seen in retrospect, evolution as a whole doubtless had a general direction, from simple to complex, from dependence on to relative independence of the environment, to greater and greater autonomy of individuals, greater and greater development of sense organs and nervous systems conveying and processing information about the state of the organism’s surroundings, and finally greater and greater consciousness. You can call this direction progress or by some other name.”
Harold Mosowitz says “Life is organization. From prokaryotic cells, eukaryotic cells, tissues and organs, to plants and animals, families, communities, ecosystems, and living planets, life is organization, at every scale. The evolution of life is the increase of biological organization, if it is anything. Clearly, if life originates and makes evolutionary progress without organizing input somehow supplied, then something has organized itself. Logical entropy in a closed system has decreased. This is the violation that people are getting at, when they say that life violates the second law of thermodynamics. This violation, the decrease of logical entropy in a closed system, must happen continually in the Darwinian account of evolutionary progress.”
Entropy occurs in all systems. That is an indisputable fact. However, if we start defining boundaries, then we are prone to see that these bounded systems decay faster. However, if we open up the system to leave it unbounded, then there are a lot of other forces that come into play that is tantamount to some net progress. While it might be true that energy balances out, what we miss as social scientists or model builders or avid students of systems – we miss out on indices that reflect on leaps in quality and resilience and a horde of other factors that stabilizes the system despite the constant and ominous presence of entropy’s inner workings.
Chaos as a system: New Framework
Chaos is not an unordered phenomenon. There is a certain homeostatic mechanism at play that forces a system that might have inherent characteristics of a “chaotic” process to converge to some sort of stability with respect to predictability and parallelism. Our understanding of order which is deemed to be opposite of chaos is the fact that there is a shared consensus that the system will behave in an expected manner. Hence, we often allude to systems as being “balanced” or “stable” or “in order” to spotlight these systems. However, it is also becoming common knowledge in the science of chaos that slight changes in initial conditions in a system can emit variability in the final output that might not be predictable. So how does one straddle order and chaos in an observed system, and what implications does this process have on ongoing study of such systems?
Chaotic systems can be considered to have a highly complex order. It might require the tools of pure mathematics and extreme computational power to understand such systems. These tools have invariably provided some insights into chaotic systems by visually representing outputs as re-occurrences of a distribution of outputs related to a given set of inputs. Another interesting tie up in this model is the existence of entropy, that variable that taxes a system and diminishes the impact on expected outputs. Any system acts like a living organism: it requires oodles of resources to survive and a well-established set of rules to govern its internal mechanism driving the vector of its movement. Suddenly, what emerges is the fact that chaotic systems display some order while subject to an inherent mechanism that softens its impact over time. Most approaches to studying complex and chaotic systems involve understanding graphical plots of fractal nature, and bifurcation diagrams. These models illustrate very complex re occurrences of outputs directly related to inputs. Hence, complex order occurs from chaotic systems.
A case in point would be the relation of a population parameter in the context to its immediate environment. It is argued that a population in an environment will maintain a certain number and there would be some external forces that will actively work to ensure that the population will maintain at that standard number. It is a very Malthusian analytic, but what is interesting is that there could be some new and meaningful influences on the number that might increase the scale. In our current meaning, a change in technology or ingenuity could significantly alter the natural homeostatic number. The fact remains that forces are always at work on a system. Some systems are autonomic – it self-organizes and corrects itself toward some stable convergence. Other systems are not autonomic and once can only resort to the laws of probability to get some insight into the possible outputs – but never to a point where there is a certainty in predictive prowess.
Organizations have a lot of interacting variables at play at any given moment. In order to influence the organization behavior or/and direction, policies might be formulated to bring about the desirable results. However, these nudges toward setting off the organization in the right direction might also lead to unexpected results. The aim is to foresee some of these unexpected results and mollify the adverse consequences while, in parallel, encourage the system to maximize the benefits. So how does one effect such changes?
It all starts with building out an operating framework. There needs to be a clarity around goals and what the ultimate purpose of the system is. Thus there are few objectives that bind the framework.
- Clarity around goals and the timing around achieving these goals. If there is no established time parameter, then the system might jump across various states over time and it would be difficult to establish an outcome.
- Evaluate all of the internal and external factors that might operate in the framework that would impact the success of organizational mandates and direction. Identify stasis or potential for stasis early since that mental model could stem the progress toward a desirable impact.
- Apply toll gates strategically to evaluate if the system is proceeding along the lines of expectation, and any early aberrations are evaluated and the rules are tweaked to get the system to track on a desirable trajectory.
- Develop islands of learning across the path and engage the right talent and other parameters to force adaptive learning and therefore a more autonomic direction to the system.
- Bind the agents and actors in the organization to a shared sense of purpose within the parameter of time.
- Introduce diversity into the framework early in the process. The engagement of diversity allows the system to modulate around a harmonic mean.
- Finally, maintain a well document knowledge base such that the accretive learning that results due to changes in the organization become springboard for new initiatives that reduces the costs of potential failures or latency in execution.
- Encouraging the leadership to ensure that the vector is pointed toward the right direction at any given time.
Once a framework and the engagement rules are drawn out, it is necessary to rely on the natural velocity and self-organization of purposeful agents to move the agenda forward, hopefully with little or no intervention. A mechanism of feedback loops along the way would guide the efficacy of the direction of the system. The implications is that the strategy and the operations must be aligned and reevaluated and positive behavior is encouraged to ensure that the systems meets its objective.
However, as noted above, entropy is a dynamic that often threatens to derail the system objective. There will be external or internal forces constantly at work to undermine system velocity. The operating framework needs to anticipate that real possibility and pre-empt that with rules or introduction of specific capital to dematerialize these occurrences. Stasis is an active agent that can work against the system dynamic. Stasis is the inclination of agents or behaviors that anchors the system to some status quo – we have to be mindful that change might not be embraced and if there are resistors to that change, the dynamic of organizational change can be invariably impacted. It will take a lot more to get something done than otherwise needed. Identifying stasis and agents of stasis is a foundational element
While the above is one example of how to manage organizations in the shadows of the properties of how chaotic systems behave, another example would be the formulation of strategy of the organization in responses to external forces. How do we apply our learnings in chaos to deal with the challenges of competitive markets by aligning the internal organization to external factors? One of the key insights that chaos surfaces is that it is nigh impossible for one to fully anticipate all of the external variables, and leaving the system to dynamically adapt organically to external dynamics would allow the organization to thrive. To thrive in this environment is to provide the organization to rapidly change outside of the traditional hierarchical expectations: when organizations are unable to make those rapid changes or make strategic bets in response to the external systems, then the execution value of the organization diminishes.
Margaret Wheatley in her book Leadership and the New Science: Discovering Order in a Chaotic World Revised says, “Organizations lack this kind of faith, faith that they can accomplish their purposes in various ways and that they do best when they focus on direction and vision, letting transient forms emerge and disappear. We seem fixated on structures…and organizations, or we who create them, survive only because we build crafty and smart—smart enough to defend ourselves from the natural forces of destruction. Karl Weick, an organizational theorist, believes that “business strategies should be “just in time…supported by more investment in general knowledge, a large skill repertoire, the ability to do a quick study, trust in intuitions, and sophistication in cutting losses.”
We can expand the notion of a chaos in a system to embrace the bigger challenges associated with environment, globalization, and the advent of disruptive technologies.
One of the key challenges to globalization is how policy makers would balance that out against potential social disintegration. As policies emerge to acknowledge the benefits and the necessity to integrate with a new and dynamic global order, the corresponding impact to local institutions can vary and might even lead to some deleterious impact on those institutions. Policies have to encourage flexibility in local institutional capability and that might mean increased investments in infrastructure, creating a diverse knowledge base, establishing rules that govern free but fair trading practices, and encouraging the mobility of capital across borders. The grand challenges of globalization is weighed upon by government and private entities that scurry to create that continual balance to ensure that the local systems survive and flourish within the context of the larger framework. The boundaries of the system are larger and incorporates many more agents which effectively leads to the real possibility of systems that are difficult to be controlled via a hierarchical or centralized body politic Decision making is thus pushed out to the agents and actors but these work under a larger set of rules. Rigidity in rules and governance can amplify failures in this process.
Related to the realities of globalization is the advent of the growth in exponential technologies. Technologies with extreme computational power is integrating and create robust communication networks within and outside of the system: the system herein could represent nation-states or companies or industrialization initiatives. Will the exponential technologies diffuse across larger scales quickly and will the corresponding increase in adoption of new technologies change the future of the human condition? There are fears that new technologies would displace large groups of economic participants who are not immediately equipped to incorporate and feed those technologies into the future: that might be on account of disparity in education and wealth, institutional policies, and the availability of opportunities. Since technologies are exponential, we get a performance curve that is difficult for us to understand. In general, we tend to think linearly and this frailty in our thinking removes us from the path to the future sooner than later. What makes this difficult is that the exponential impact is occurring across various sciences and no one body can effectively fathom the impact and the direction. Bill Gates says it well “We always overestimate the change that will occur in the next two years and underestimate the change that will occur in the next ten. Don’t let yourself be lulled into inaction.” Does chaos theory and complexity science arm us with a differentiated tool set than the traditional toolset of strategy roadmaps and product maps? If society is being carried by the intractable and power of the exponent in advances in technology, than a linear map might not serve to provide the right framework to develop strategies for success in the long-term. Rather, a more collaborative and transparent roadmap to encourage the integration of thoughts and models among the actors who are adapting and adjusting dynamically by the sheer force of will would perhaps be an alternative and practical approach in the new era.
Lately there has been a lot of discussion around climate change. It has been argued, with good reason and empirical evidence, that environment can be adversely impacted on account of mass industrialization, increase in population, resource availability issues, the inability of the market system to incorporate the cost of spillover effects, the adverse impact of moral hazard and the theory of the commons, etc. While there are demurrers who contest the long-term climate change issues, the train seems to have already left the station! The facts do clearly reflect that the climate will be impacted. Skeptics might argue that science has not yet developed a precise predictive model of the weather system two weeks out, and it is foolhardy to conclude a dystopian future on climate fifty years out. However, the alternative argument is that our inability to exercise to explain the near-term effects of weather changes and turbulence does not negate the existence of climate change due to the accretion of greenhouse impact. Boiling a pot of water will not necessarily gives us an understanding of all of the convection currents involved among the water molecules, but it certainly does not shy away from the fact that the water will heat up.
History of Chaos
| Chaos is inherent in all compounded things. Strive on with diligence! –Buddha |
Scientific theories are characterized by the fact that they are open to refutation. To create a scientific model, there are three successive steps that one follows: observe the phenomenon, translate that into equations, and then solve the equations.
One of the early philosophers of science, Karl Popper (1902-1994) discussed this at great length in his book – The Logic of Scientific Discovery. He distinguishes scientific theories from metaphysical or mythological assertions. His main theses is that a scientific theory must be open to falsification: it has to be reproducible separately and yet one can gather data points that might refute the fundamental elements of theory. Developing a scientific theory in a manner that can be falsified by observations would result in new and more stable theories over time. Theories can be rejected in favor of a rival theory or a calibration of the theory in keeping with the new set of observations and outcomes that the theories posit. Until Popper’s time and even after, social sciences have tried to work on a framework that would allow the construction of models that would formulate some predictive laws that govern social dynamics. In his book, Poverty of Historicism, Popper maintained that such an endeavor is not fruitful since it does not take into consideration the myriad of minor elements that interact closely with one another in a meaningful way. Hence, he has touched indirectly on the concept of chaos and complexity and how it touches the scientific method. We will now journey into the past and through the present to understand the genesis of the theory and how it has been channelized by leading scientists and philosophers to decipher a framework for study society and nature.
As we have already discussed, one of the main pillars of Science is determinism: the probability of prediction. It holds that every event is determined by natural laws. Nothing can happen without an unbroken chain of causes that can be traced all the way back to an initial condition. The deterministic nature of science goes all the way back to Aristotelian times. Interestingly, Aristotle argued that there is some degree of indeterminism and he relegated this to chance or accidents. Chance is a character that makes its presence felt in every plot in the human and natural condition. Aristotle wrote that “we do not have knowledge of a thing until we have grasped its why, that is to say, its cause.” He goes on to illustrate his idea in greater detail – namely, that the final outcome that we see in a system is on account of four kinds of influencers: Matter, Form, Agent and Purpose.
Matter is what constitutes the outcome. For a chair it might be wood. For a statue, it might be marble. The outcome is determined by what constitutes the outcome.
Form refers to the shape of the outcome. Thus, a carpenter or a sculptor would have a pre-conceived notion of the shape of the outcome and they would design toward that artifact.
Agent refers to the efficient cause or the act of producing the outcome. Carpentry or masonry skills would be important to shape the final outcome.
Finally, the outcome itself must serve a purpose on its own. For a chair, it might be something to sit on, for a statue it might be something to be marveled at.
However, Aristotle also admits that luck and chance can play an important role that do not fit the causal framework in its own right. Some things do happen by chance or luck. Chance is a rare event, it is a random event and it is typically brought out by some purposeful action or by nature.
We had briefly discussed the Laplace demon and he summarized this wonderfully: “We ought then to consider the resent state of the universe as the effect of its previous state and as the cause of that which is to follow. An intelligence that, at a given instant, could comprehend all the forces by which nature is animated and the respective situation of the beings that make it up if moreover it were vast enough to submit these data to analysis, would encompass in the same formula the movements of the greatest bodies of the universe and those of the lightest atoms. For such an intelligence nothing would be uncertain, and the future, like the past, would be open to its eyes.” He thus admits to the fact that we lack the vast intelligence and we are forced to use probabilities in order to get a sense of understanding of dynamical systems.
It was Maxwell in his pivotal book “Matter and Motion” published in 1876 lay the groundwork of chaos theory.
“There is a maxim which is often quoted, that “the same causes will always produce the same effects.’ To make this maxim intelligible we must define what we mean by the same causes and the same effects, since it is manifest that no event ever happens more than once, so that the causes and effects cannot be the same in all respects. There is another maxim which must not be confounded with that quoted at the beginning of this article, which asserts “That like causes produce like effects.” This is only true when small variations in the initial circumstances produce only small variations in the final state of the system. In a great many physical phenomena this condition is satisfied: but there are other cases in which a small initial variation may produce a great change in the final state of the system, as when the displacement of the points cause a railway train to run into another instead of keeping its proper course.” What is interesting however in the above quote is that Maxwell seems to go with the notion that in a great many cases there is no sensitivity to initial conditions.
In the 1890’s Henri Poincare was the first exponent of chaos theory. He says “it may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible.” This was a far cry from the Newtonian world which sought order on how the solar system worked. Newton’s model was posted on the basis of the interaction between just two bodies. What would then happen if three bodies or N bodies were introduced into the model. This led to the rise of the Three Body Problem which led to Poincare embracing the notion that this problem could not be solved and can be tackled by approximate numerical techniques. Solving this resulted in solutions that were so tangled that is was difficult to not only draw them, it was near impossible to derive equations to fit the results. In addition, Poincare also discovered that if the three bodies started from slightly different initial positions, the orbits would trace out different paths. This led to Poincare forever being designated as the Father of Chaos Theory since he laid the groundwork on the most important element in chaos theory which is the sensitivity to initial dependence.
In the early 1960’s, the first true experimenter in chaos was a meteorologist named Edward Lorenz. He was working on a problem in weather prediction and he set up a system with twelve equations to model the weather. He set the initial conditions and the computer was left to predict what the weather might be. Upon revisiting this sequence later on, he inadvertently and by sheer accident, decided to run the sequence again in the middle and he noticed that the outcome was significantly different. The imminent question that followed was why the outcome was so different than the original. He traced this back to the initial condition wherein he noted that the initial input was different with respect to the decimal places. The system incorporated the all of the decimal places rather than the first three. (He had originally input the number .506 and he had concatenated the number from .506127). He would have expected that this thin variation in input would have created a sequence close to the original sequence but that was not to be: it was distinctly and hugely different. This effect became known as the Butterfly effect which is often substituted for Chaos Theory. Ian Stewart in his book, Does God Play Dice? The Mathematics of Chaos, describes this visually as follows:
“The flapping of a single butterfly’s wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month’s time, a tornado that would have devastated the Indonesian cost doesn’t happen. Or maybe one that wasn’t going to happen, does.”
Lorenz thus argued that it would be impossible to predict the weather accurately. However, he reduced his experiment to fewer set of equations and took upon observations of how small change in initial conditions affect predictability of smaller systems. He found a parallel – namely, that changes in initial conditions tends to render the final outcome of a system to be inaccurate. As he looked at alternative systems, he found a strange pattern that emerged – namely, that the system always represented a double spiral – the system never settled down to a single point but they never repeated its trajectory. It was a path breaking discovery that led to further advancement in the science of chaos in later years.
Years later, Robert May investigated how this impacts population. He established an equation that reflected a population growth and initialized the equation with a parameter for growth rate value. (The growth rate was initialized to 2.7). May found that as he increased the parameter value, the population grew which was expected. However, once he passed the 3.0 growth value, he noticed that equation would not settle down to a single population but branch out to two different values over time. If he raised the initial value more, the bifurcation or branching of the population would be twice as much or four different values. If he continued to increase the parameter, the lines continue to double until chaos appeared and it became hard to make point predictions.
There was another innate discovery that occurred through the experiment. When one visually looks at the bifurcation, one tends to see similarity between the small and large branches. This self-similarity became an important part of the development of chaos theory.
Benoit Mandelbrot started to study this self-similarity pattern in chaos. He was an economist and he applied mathematical equations to predict fluctuations in cotton prices. He noted that particular price changes were not predictable but there were certain patterns that were repeated and the degree of variation in prices had remained largely constant. This is suggestive of the fact that one might, upon preliminary reading of chaos, arrive at the notion that if weather cannot be predictable, then how can we predict climate many years out. On the contrary, Mandelbrot’s experiments seem to suggest that short time horizons are difficult to predict that long time horizon impact since systems tend to settle into some patterns that is reflecting of smaller patterns across periods. This led to the development of the concept of fractal dimensions, namely that sub-systems develop a symmetry to a larger system.
Feigenbaum was a scientist who became interested in how quickly bifurcations occur. He discovered that regardless of the scale of the system, the came at a constant rate of 4.669. If you reduce or enlarge the scale by that constant, you would see the mechanics at work which would lead to an equivalence in self-similarity. He applied this to a number of models and the same scaling constant took effect. Feigenbaum had established, for the first time, a universal constant around chaos theory. This was important because finding a constant in the realm of chaos theory was suggestive of the fact that chaos was an ordered process, not a random one.
Sir James Lighthill gave a lecture and in that he made an astute observation –
“We are all deeply conscious today that the enthusiasm of our forebears for the marvelous achievements of Newtonian mechanics led them to make generalizations in this area of predictability which, indeed, we may have generally tended to believe before 1960, but which we now recognize were false. We collectively wish to apologize for having misled the general educated public by spreading ideas about determinism of systems satisfying Newton’s laws of motion that, after 1960, were to be proved incorrect.”
Managing Scale
| I think the most difficult thing had been scaling the infrastructure. Trying to support the response we had received from our users and the number of people that were interested in using the software. – Shawn Fanning |
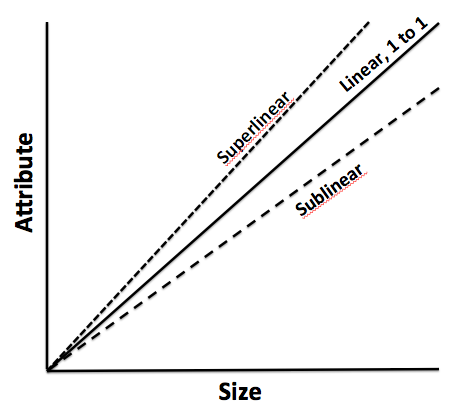
Froude’s number? It is defined as the square of the ship’s velocity divided by its length and multiplied by the acceleration caused by gravity. So why are we introducing ships in this chapter? As I have done before, I am liberally standing on the shoulder of the giant, Geoffrey West, and borrowing from his account on the importance of the Froude’s number and the practical implications. Since ships are subject to turbulence, using a small model that works in a simulated turbulent environment might not work when we manufacture a large ship that is facing the ebbs and troughs of a finicky ocean. The workings and impact of turbulence is very complex, and at scale it becomes even more complex. Froude’s key contribution was to figure out a mathematical pathway of how to efficiently and effectively scale from a small model to a practical object. He did that by using a ratio as the common denominator. Mr. West provides an example that hits home: How fast does a 10-foot-long ship have to move to mimic the motion of a 700-foot-long ship moving at 20 knots. If they are to have the same Froude number (that is, the same value of the square of their velocity divided by their length), then the velocity has to scale as the square root of their lengths. The ratio of the square root of their lengths is the the square of 700 feet of the ship/10 feet of the model ship which turns out to be the square of 70. For the 10-foot model to mimic the motion of a large ship, it must move at the speed of 20 knots/ square of 70 or 2.5 knots. The Froude number is still widely used across many fields today to bridge small scale and large-scale thinking. Although this number applies to physical systems, the notion that adaptive systems can be similarly bridged through appropriate mathematical equations. Unfortunately, because of the increased number of variables impacting adaptive systems and all of these variables working and learning from one another, the task of establishing a Froude number becomes diminishingly small.
The other concept that has gained wide attention is the science of allometry. Allometry essentially states that as size increases, then the form of the object would change. Allometric scaling governs all complex physical and adaptive systems. So the question is whether there are some universal laws or mathematics that can be used to enable us to better understand or predict scale impacts. Let us extend this thinking a bit further. If sizes influence form and form constitute all sub-physical elements, then it would stand to reason that a universal law or a set of equations can provide deep explanatory powers on scale and systems. One needs to bear in mind that even what one might consider a universal law might be true within finite observations and boundaries. In other words, if there are observations that fall outside of those boundaries, one is forced into resetting our belief in the universal law or to frame a new paradigm to cover these exigencies. I mention this because as we seek to understand business and global grand challenges considering the existence of complexity, scale, chaos and seeming disorder – we might also want to embrace multiple laws or formulations working at different hierarchies and different data sets to arrive at satisficing solutions to the problems that we want to wrestle with.
Physics and mathematics allow a qualitatively high degree of predictability. One can craft models across different scales to make a sensible approach on how to design for scale. If you were to design a prototype using a 3D printer and decide to scale that prototype a 100X, there are mathematical scalar components that are factored into the mechanics to allow for some sort of equivalence which would ultimately lead to the final product fulfilling its functional purpose in a complex physical system. But how does one manage scale in light of those complex adaptive systems that emerge due to human interactions, evolution of organization, uncertainty of the future, and dynamic rules that could rapidly impact the direction of a company?
Is scale a single measure? Or is it a continuum? In our activities, we intentionally or unintentionally invoke scale concepts. What is the most efficient scale to measure an outcome, so we can make good policy decisions, how do we apply our learning from one scale to a system that operates on another scale and how do we assess how sets of phenomena operate at different scales, spatially and temporally, and how they impact one another? Now the most interesting question: Is scale polymorphous? Does the word scale have different meanings in different contexts? When we talk about microbiology, we are operating at micro-scales. When we talk at a very macro level, our scales are huge. In business, we regard scale with respect to how efficiently we grow. In one way, it is a measure but for the following discussion, we will interpret scale as non-linear growth expending fewer and fewer resources to support that growth as a ratio.
As we had discussed previously, complex adaptive systems self-organize over time. They arrive at some steady state outcome without active intervention. In fact, the active intervention might lead to unintended consequences that might even spell doom for the system that is being influenced. So as an organization scales, it is important to keep this notion of rapid self-organization in mind which will inform us to make or not make certain decisions from a central or top-down perspective. In other words, part of managing scale successfully is to not manage it at a coarse-grained level.
The second element of successfully managing scale is to understand the constraints that prevent scale. There is an entire chapter dedicated to the theory of constraints which sheds light on why this is a fundamental process management technique that increases the pace of the system. But for our purposes in this section, we will summarize as follows: every system as it grows have constraints. It is important to understand the constraints because these constraints slow the system: the bottlenecks have to be removed. And once one constraint is removed, then one comes across another constraint. The system is a chain of events and it is imperative that all of these events are identified. The weakest links harangue the systems and these weakest links have to be either cleared or resourced to enable the system to scale. It is a continuous process of observation and tweaking the results with the established knowledge that the demons of uncertainty and variability can reset the entire process and one might have to start again. Despite that fact, constraint management is an effective method to negotiate and manage scale.
The third element is devising the appropriate organization architecture. As one projects into the future, management might be inclined toward developing and investing in the architecture early to accommodate the scale. Overinvestment in the architecture might not be efficient. As mentioned, cities and social systems that grow 100% require 85% investment in infrastructure: in other words, systems grow on a sublinear scale from an infrastructure perspective. How does management of scale arrive at the 85%? It is nigh impossible, but it is important to reserve that concept since it informs management to architect the infrastructure cautiously. Large investments upfront could be a waste or could slow the system down: alternative, investments that are postponed a little too late can also impact the system adversely.
The fourth element of managing scale is to focus your lens of opportunity. In macroecology, we can arrive at certain conclusions when we regard the system from a distance versus very closely. We can subsume our understanding into one big bucket called climate change and then we figure out different ways to manage the complexity that causes the climate change by invoking certain policies and incentives at a macro level. However, if we go closer, we might decide to target a very specific contributor to climate change – namely, fossil fuels. The theory follows that to manage the dynamic complexity and scale of climate impact – it would be best to address a major factor which, in this case, would be fossil fuels. The equivalence of this in a natural business setting would be to establish and focus the strategy for scale in a niche vertical or a relatively narrower set of opportunities. Even though we are working in the web of complex adaptive systems, we might devise strategies to directionally manage the business within the framework of complex physical systems where we have an understanding of the slight variations of initial state and the realization that the final outcome might be broad but yet bounded for intentional management.
The final element is the management of initial states. Complex physical systems are governed by variation in initial states. Perturbation of these initial states can lead to a wide divergence of outcomes, albeit bounded within a certain frame of reference. It is difficult perhaps to gauge all the interactions that might occur from a starting point to the outcome, although we agree that a few adjustments like decentralization of decision making, constraint management, optimal organization structure and narrowing the playing field would be helpful.
Internal versus External Scale
This article discusses internal and external complexity before we tee up a more detailed discussion on internal versus external scale. This chapter acknowledges that complex adaptive systems have inherent internal and external complexities which are not additive. The impact of these complexities is exponential. Hence, we have to sift through our understanding and perhaps even review the salient aspects of complexity science which have already been covered in relatively more detail in earlier chapter. However, revisiting complexity science is important, and we will often revisit this across other blog posts to really hit home the fundamental concepts and its practical implications as it relates to management and solving challenges at a business or even a grander social scale.
A complex system is a part of a larger environment. It is a safe to say that the larger environment is more complex than the system itself. But for the complex system to work, it needs to depend upon a certain level of predictability and regularity between the impact of initial state and the events associated with it or the interaction of the variables in the system itself. Note that I am covering both – complex physical systems and complex adaptive systems in this discussion. A system within an environment has an important attribute: it serves as a receptor to signals of external variables of the environment that impact the system. The system will either process that signal or discard the signal which is largely based on what the system is trying to achieve. We will dedicate an entire article on system engineering and thinking later, but the uber point is that a system exists to serve a definite purpose. All systems are dependent on resources and exhibits a certain capacity to process information. Hence, a system will try to extract as many regularities as possible to enable a predictable dynamic in an efficient manner to fulfill its higher-level purpose.
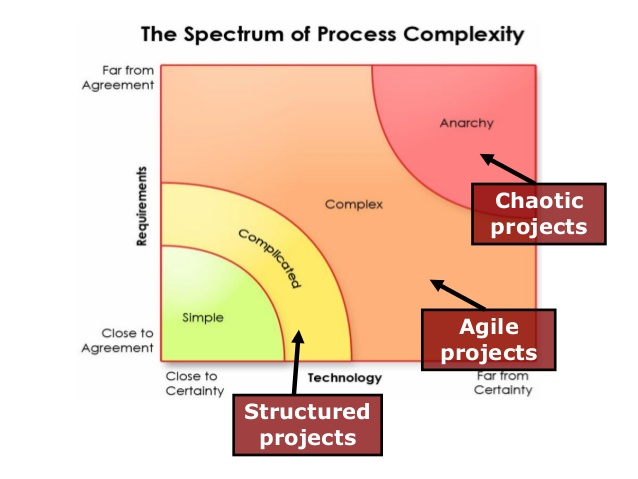
Let us understand external complexities. We can interchangeably use the word environmental complexity as well. External complexity represents physical, cultural, social, and technological elements that are intertwined. These environments beleaguered with its own grades of complexity acts as a mold to affect operating systems that are mere artifacts. If operating systems can fit well within the mold, then there is a measure of fitness or harmony that arises between an internal complexity and external complexity. This is the root of dynamic adaptation. When external environments are very complex, that means that there are a lot of variables at play and thus, an internal system has to process more information in order to survive. So how the internal system will react to external systems is important and they key bridge between those two systems is in learning. Does the system learn and improve outcomes on account of continuous learning and does it continually modify its existing form and functional objectives as it learns from external complexity? How is the feedback loop monitored and managed when one deals with internal and external complexities? The environment generates random problems and challenges and the internal system has to accept or discard these problems and then establish a process to distribute the problems among its agents to efficiently solve those problems that it hopes to solve for. There is always a mechanism at work which tries to align the internal complexity with external complexity since it is widely believed that the ability to efficiently align the systems is the key to maintaining a relatively competitive edge or intentionally making progress in solving a set of important challenges.
Internal complexity are sub-elements that interact and are constituents of a system that resides within the larger context of an external complex system or the environment. Internal complexity arises based on the number of variables in the system, the hierarchical complexity of the variables, the internal capabilities of information pass-through between the levels and the variables, and finally how it learns from the external environment. There are five dimensions of complexity: interdependence, diversity of system elements, unpredictability and ambiguity, the rate of dynamic mobility and adaptability, and the capability of the agents to process information and their individual channel capacities.
If we are discussing scale management, we need to ask a fundamental question. What is scale in the context of complex systems? Why do we manage for scale? How does management for scale advance us toward a meaningful outcome? How does scale compute in internal and external complex systems? What do we expect to see if we have managed for scale well? What does the future bode for us if we assume that we have optimized for scale and that is the key objective function that we have to pursue?
Scaling Considerations in Complex Systems and Organizations: Implications
Scale represents size. In a two-dimensional world, it is a linear measurement that presents a nominal ordering of numbers. In other words, 4 is two times two and 6 would be 3 times two. In other words, the difference between 4 and 6 represents an increase in scale by two. We will discuss various aspects of scale and the learnings that we can draw from it. However, before we go down this path, we would like to touch on resource consumption.
As living organisms, we consume resources. An average human being requires 2000 calories of food per day to sustain themselves. An average human being, by the way, is largely defined in terms of size. So it would be better put if we say that a 200lb person would require 2000 calories. However, if we were to regard a specimen that is 10X the size or 2000 lbs., would it require 10X the calories to sustain itself? Conversely, if the specimen was 1/100th the size of the average human being, then would it require 1/100th the calories to sustain itself. Thus, will we consume resources linearly to our size? Are we operating in a simple linear world? And if not, what are the ramifications for science, physics, biology, organizations, cities, climate, etc.?
Let us digress a little bit from the above questions and lay out a few interesting facts. Almost half of the population in the world today live in cities. This is compared to less than 15% of the world population that lived in cities a hundred years ago. It is anticipated that almost 75% of the world population will be living in cities by 2050. The number of cities will increase and so will the size. But for cities to increase in size and numbers, it requires vast amount of resources. In fact, the resource requirements in cities are far more extensive than in agrarian societies. If there is a limit to the resources from a natural standpoint – in other words, if the world is operating on a budget of natural resources – then would this mean that the growth of the cities will be naturally reined in? Will cities collapse because of lack of resources to support its mass?
What about companies? Can companies grow infinitely? Is there a natural point where companies might hit their limit beyond which growth would not be possible? Could a company collapse because the amount of resources that is required to sustain the size would be compromised? Are there other factors aside from resource consumption that play into what might cap the growth and hence the size of the company? Are there overriding factors that come into play that would superimpose the size-resource usage equation such that our worries could be safely kept aside? Are cities and companies governed by some sort of metabolic rate that governs the sustenance of life?
Geoffrey West, a theoretical physicist, has touched on a lot of the questions in his book: Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies. He says that a person requires about 90W (watts) of energy to survive. That is a light bulb burning in your living room in one day. That is our metabolic rate. However, just like man does not live by bread alone, an average man has to depend on a number of other artifacts that have agglomerated in bits and pieces to provide a quality of life to maximize sustenance. The person has to have laws, electricity, fuel, automobile, plumbing and water, markets, banks, clothes, phones and engage with other folks in a complex social network to collaborate and compete to achieve their goals. Geoffrey West says that the average person requires almost 11000W or the equivalent of almost 125 90W light bulbs. To put things in greater perspective, the social metabolic rate of 11,000W is almost equivalent to a dozen elephants. (An elephant requires 10X more energy than humans even though they might be 60X the size of the physical human being). Thus, a major portion of our energy is diverted to maintain the social and physical network that closely interplay to maintain our sustenance. And while we consume massive amounts of energy, we also create a massive amount of waste – and that is an inevitable outcome. This is called the entropy impact and we will touch on this in greater detail in later articles. Hence, our growth is not only constrained by our metabolic rate: it is further dampened by entropy that exists as the Second Law of Thermodynamics. And as a system ages, the impact of entropy increases manifold. Yes, it is true: once we get old, we are racing toward our death at a faster pace than when we were young. Our bodies are exhibiting fatigue faster than normal.
Scaling refers to how a system responds when its size changes. As mentioned earlier, does scaling follow a linear model? Do we need to consume 2X resources if we increase the size by 2X? How does scaling impact a Complex Physical System versus a Complex Adaptive System? Will a 2X impact on the initial state create perturbations in a CPS model which is equivalent to 2X? How would this work on a CAS model where the complexity is far from defined and understood because these systems are continuously evolving? Does half as big requires half as much or conversely twice as big requires twice as much? Once again, I have liberally dipped into this fantastic work by Geoffrey West to summarize, as best as possible, the definitions and implications. He proves that we cannot linearly extrapolate energy consumption and size: the world is smattered with evidence that undermines the linear extrapolation model. In fact, as you grow, you become more efficient with respect to energy consumption. The savings of energy due to growth in size is commonly called the economy of scale. His research also suggests two interesting results. When cities or social systems grow, they require an infrastructure to help with the growth. He discovered that it takes 85% resource consumption to grow the systems by 100%. Thus, there is a savings of 15% which is slightly lower than what has been studied on the biological front wherein organisms save 25% as they grow. He calls this sub linear scaling. In contrast, he also introduces the concept of super linear scaling wherein there is a 15% increasing returns to scale when the city or a social system grows. In other words, if the system grows by 100%, the positive returns with respect to such elements like patents, innovation, etc. will grow by 115%. In addition, the negative elements also grow in an equivalent manner – crime, disease, social unrest, etc. Thus, the growth in cities are supported by an efficient infrastructure that generates increasing returns of good and bad elements.
Max Kleiber, a Swiss chemist, in the 1930’s proposed the Kleiber’s law which sheds a lot of light on metabolic rates as energy consumption per unit of time. As mass increases so does the overall metabolic rate but it is not a linear relation – it obeys the power law. It stays that a living organism’s metabolic rate scales to the ¾ power of its mass. If the cat has a mass 100 times that of a mouse, the cat will metabolize about 100 ¾ = 31.63 times more energy per day rather than 100 times more energy per day. Kleiber’s law has led to the metabolic theory of energy and posits that the metabolic rate of organisms is the fundamental biological rate that governs most observed patters in our immediate ecology. There is some ongoing debate on the mechanism that allows metabolic rate to differ based on size. One mechanism is that smaller organisms have higher surface area to volume and thus needs relatively higher energy versus large organisms that have lower surface area to volume. This assumes that energy consumption occurs across surface areas. However, there is another mechanism that argues that energy consumption happens when energy needs are distributed through a transport network that delivers and synthesizes energy. Thus, smaller organisms do not have as a rich a network as large organisms and thus there is greater energy efficiency usage among smaller organisms than larger organisms. Either way, the implications are that body size and temperature (which is a result of internal activity) provide fundamental and natural constraints by which our ecological processes are governed. This leads to another concept called finite time singularity which predicts that unbounded growth cannot be sustained because it would need infinite resources or some K factor that would allow it to increase. The K factor could be innovation, a structural shift in how humans and objects cooperate, or even a matter of jumping on a spaceship and relocating to Mars.
We are getting bigger faster. That is real. The specter of a dystopian future hangs upon us like the sword of Damocles. The thinking is that this rate of growth and scale is not sustainable since it is impossible to marshal the resources to feed the beast in an adequate and timely manner. But interestingly, if we were to dig deeper into history – these thoughts prevailed in earlier times as well but perhaps at different scale. In 1798 Thomas Robert Malthus famously predicted that short-term gains in living standards would inevitably be undermined as human population growth outstripped food production, and thereby drive living standards back toward subsistence. Humanity thus was checkmated into an inevitable conclusion: a veritable collapse spurred by the tendency of population to grow geometrically while food production would increase only arithmetically. Almost two hundred years later, a group of scientists contributed to the 1972 book called Limits to Growth which had similar refrains like Malthus: the population is growing and there are not enough resources to support the growth and that would lead to the collapse of our civilization. However, humanity has negotiated those dark thoughts and we continue to prosper. If indeed, we are governed by this finite time singularity, we are aware that human ingenuity has largely won the day. Technology advancements, policy and institutional changes, new ways of collaboration, etc. have emerged to further delay this “inevitable collapse” that could be result of more mouths to feed than possible. What is true is that the need for new innovative models and new ways of doing things to solve the global challenges wrought by increased population and their correspondent demands will continue to increase at a quicker pace. Once could thus argue that the increased pace of life would not be sustainable. However, that is not a plausible hypothesis based on our assessment of where we are and where we have been.
Let us turn our attention to a business. We want the business to grow or do we want the business to scale? What is the difference? To grow means that your company is adding resources or infrastructure to handle increased demand, at a cost which is equivalent to the level of increased revenue coming in. Scaling occurs when the business is growing faster than the resources that are being consumed. We have already explored that outlier when you grow so big that you are crushed by your weight. It is that fact which limits the growth of organism regardless of issues related to scale. Similarly, one could conceivably argue that there are limits to growth of a company and might even turn to history and show that a lot of large companies of yesteryears have collapsed. However, it is also safe to say that large organizations today are by several factors larger than the largest organizations in the past, and that is largely on account of accumulated knowledge and new forms of innovation and collaboration that have allowed that to happen. In other words, the future bodes well for even larger organizations and if those organizations indeed reach those gargantuan size, it is also safe to draw the conclusion that they will be consuming far less resources relative to current organizations, thus saving more energy and distributing more wealth to the consumers.
Thus, scaling laws limit growth when it assumes that everything else is constant. However, if there is innovation that leads to structural changes of a system, then the limits to growth becomes variable. So how do we effect structural changes? What is the basis? What is the starting point? We look at modeling as a means to arrive at new structures that might allow the systems to be shaped in a manner such that the growth in the systems are not limited by its own constraints of size and motion and temperature (in physics parlance). Thus, a system is modeled at a presumably small scale but with the understanding that as the system is increases in size, the inner workings of emergent complexity could be a problem. Hence, it would be prudent to not linearly extrapolate the model of a small system to that of a large one but rather to exponential extrapolate the complexity of the new system that would emerge. We will discuss this in later articles, but it would be wise to keep this as a mental note as we forge ahead and refine our understanding of scale and its practical implications for our daily consumption.
Linked Stars Blog 